
分析 $\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$两两所成的角均为120°,|$\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$|=$\sqrt{(\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c})^{2}}$,由此能求出结果.
解答 解:∵向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$彼此不共线,且$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$两两所成的角相等,
|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=1,|$\overrightarrow{c}$|=3,
∴|$\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$|=$\sqrt{(\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c})^{2}}$
=$\sqrt{{\overrightarrow{a}}^{2}+{\overrightarrow{b}}^{2}+{\overrightarrow{c}}^{2}+2|\overrightarrow{a}|•|\overrightarrow{b}|cos120°+2|\overrightarrow{a}|•|\overrightarrow{c}|cos120°+2|\overrightarrow{b}|•|\overrightarrow{c}|cos120°}$
=$\sqrt{1+1+9-\frac{1}{2}-\frac{3}{2}-\frac{3}{2}}$
=$\frac{\sqrt{30}}{2}$.
故答案为:$\frac{\sqrt{30}}{2}$.
点评 本题考查向量和的模的求法,是中档题,解题时要认真审题,注意向量的性质的合理运用.


 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:选择题
| A. | 极大值为6,极大值为-26 | B. | 极大值为5,极大值为-26 | ||
| C. | 极大值为6,极大值为-25 | D. | 极大值为5,极大值为-25 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
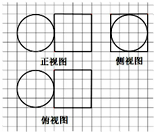
| A. | $\frac{32π}{3}$ | B. | 64+$\frac{32π}{3}$ | C. | 16π | D. | 64+$\frac{256π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 560 | B. | 527 | C. | 2015 | D. | 630 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 60° | C. | 90° | D. | 45° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com