
分析 (1)运用向量的数量积的坐标表示和二倍角的余弦公式及两角和的正弦公式,结合正弦函数的图象和性质,即可得到所求函数的值域;
(2)由题意可得sin(2x+$\frac{π}{4}$)=$\frac{k}{\sqrt{2}}$,讨论当0<k<$\sqrt{2}$时,当k=0时,结合函数的对称性和周期性,即可得到所求所求实根之和.
解答 解:(1)向量$\overrightarrow{a}$=(2cos2x,1),$\overrightarrow{b}$=(1,sin2x),
函数f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$-1=2cos2x+sin2x-1=cos2x+sin2x=$\sqrt{2}$sin(2x+$\frac{π}{4}$),
x∈[0,$\frac{π}{2}$],2x+$\frac{π}{4}$∈[$\frac{π}{4}$,$\frac{5π}{4}$],
可得sin(2x+$\frac{π}{4}$)∈[-$\frac{\sqrt{2}}{2}$,1],
即有函数f(x)的值域为[-1,$\sqrt{2}$];
(2)方程f(x)=k,(0$≤k<\sqrt{2}$),
可得sin(2x+$\frac{π}{4}$)=$\frac{k}{\sqrt{2}}$,
由y=sin(2x+$\frac{π}{4}$)的周期为π,
[-$\frac{π}{8}$,$\frac{15π}{8}$]为2个周期,
当0<k<$\sqrt{2}$时,即0<$\frac{k}{\sqrt{2}}$<1时,sin(2x+$\frac{π}{4}$)=$\frac{k}{\sqrt{2}}$在[-$\frac{π}{8}$,$\frac{15π}{8}$]内有4个交点,
即有4个不等实根,根据图象的对称性,可得x1+x2=$\frac{π}{4}$,x3+x4=$\frac{9π}{4}$,
所有实根的和为x1+x2+x3+x4=$\frac{5π}{2}$;
当k=0时,sin(2x+$\frac{π}{4}$)=0在[-$\frac{π}{8}$,$\frac{15π}{8}$]内有5个交点,
所有实根的和为x1+x2+x3+x4+x5=-$\frac{π}{8}$+$\frac{3π}{8}$+$\frac{7π}{8}$+$\frac{11π}{8}$+$\frac{15π}{8}$=$\frac{35π}{8}$.
点评 本题考查三角函数的恒等变换和三角函数的值域和对称性,考查向量数量积的坐标表示,以及分类讨论思想方法和运算能力,属于中档题.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,x2+1≤0 | B. | ?x∈R,x2+1<0 | C. | ?x∈R,x2+1<0 | D. | ?x∈R,x2+1≤0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
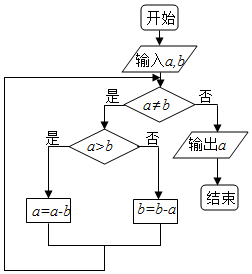 《九章算术》是我国古代数学名著,汇集古人智慧,其中的“更相减损术”更是有着深刻的应用.如图所示程序框图的算法思想即来源于此,若输入的a=2016,输出的a=21,则输入的b可能为( )
《九章算术》是我国古代数学名著,汇集古人智慧,其中的“更相减损术”更是有着深刻的应用.如图所示程序框图的算法思想即来源于此,若输入的a=2016,输出的a=21,则输入的b可能为( )| A. | 288 | B. | 294 | C. | 378 | D. | 399 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{12}$ | B. | $\frac{1}{2}$ | C. | $\frac{7}{12}$ | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com