Question

1．已知双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右焦点为F（c，0），双曲线C上一点N满足|ON|=c，若双曲线的一条渐近线平分∠FON，则双曲线的两条渐近线方程是y=±2x．

Answer 1

分析 设双曲线的左焦点为F'，连接NF'，可得NF'与渐近线平行，即有NF⊥NF'，设|NF'|=m，运用双曲线的定义和正切函数的定义，求得m，再由勾股定理和渐近线方程，即可得到所求．

解答 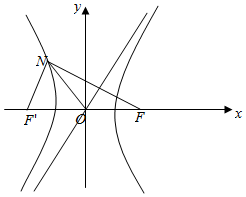解：设双曲线的左焦点为F'，连接NF'，
由双曲线的渐近线y=$\frac{b}{a}$x垂直平分线段NF'，
可得NF'与渐近线平行，即有NF⊥NF'，
设|NF'|=m，由双曲线的定义可得|NF|=2a+m，
由渐近线的斜率可得tan∠NF'F=$\frac{b}{a}$=$\frac{m+2a}{m}$，
解得m=$\frac{2{a}^{2}}{b-a}$，
在直角三角形NFF'中，可得
（2c）²=m²+（2a+m）²，
即有4c²=（$\frac{2{a}^{2}}{b-a}$）²+（$\frac{2ab}{b-a}$）²，
由c²=a²+b²，
化简可得（b-a）²=a²，
即为b=2a，
则双曲线的两条渐近线方程是y=±$\frac{b}{a}$x，
即为y=±2x．
故答案为：y=±2x．

点评 本题考查双曲线的渐近线方程的求法，注意运用双曲线的定义和垂直平分线的性质，以及勾股定理，考查化简整理的运算能力，属于中档题．