
分析 (1)利用周期公式求f(x)的最小正周期,利用当$x=\frac{π}{12}$时,f(x)有最大值2,求出解析式;
(2)若$f(α+\frac{π}{3})=-\frac{1}{2},α∈[0,\frac{π}{4}]$,求出cos2α,即可求$f(α+\frac{π}{6})$的值.
解答 解:(1)$T=\frac{2π}{ω}=\frac{2π}{2}=π$,
当$x=\frac{π}{12}$时,f(x)有最大值2,又$A>0,0<ϕ<\frac{π}{2}$,∴A=2,
∴$2×\frac{π}{12}+ϕ=\frac{π}{2}$,即$ϕ=\frac{π}{3}$,所以f(x)的解析式为$f(x)=2sin(2x+\frac{π}{3})$.
(2)∵$f(α+\frac{π}{3})=2sin(2(α+\frac{π}{3})+\frac{π}{3})=-2sin2α=-\frac{1}{2}$,∴$sin2α=\frac{1}{4}$,
∵$α∈[0,\frac{π}{4}]$,则$2α∈[0,\frac{π}{2}]$,∴$cos2α=\frac{{\sqrt{15}}}{4}$,
∴$f(α+\frac{π}{6})=2sin(2(α+\frac{π}{6})+\frac{π}{3})=2sin(2α+\frac{2π}{3})$,
∴$f(α+\frac{π}{6})=2sin2αcos\frac{2π}{3}+2cos2αsin\frac{2π}{3}=2×\frac{1}{4}×(-\frac{1}{2})+2×\frac{{\sqrt{15}}}{4}×\frac{{\sqrt{3}}}{2}=\frac{{3\sqrt{5}-1}}{4}$.
点评 本题考查三角函数的图象与性质,考查诱导公式的运用,正确求出函数的解析式是关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | $\frac{4}{3}$ | C. | $\frac{25}{6}$ | D. | 不存在 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 54 | B. | 55 | C. | 56 | D. | 57 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
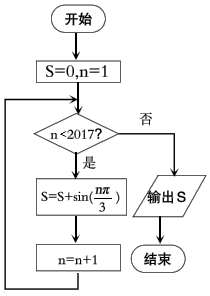
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $-\frac{{\sqrt{3}}}{2}$ | C. | $\sqrt{3}$ | D. | 0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com