Question

18．我们知道，以正三角形的三边中点为顶点的三角形与原三角形的面积之比为1：4，类比该命题得，以正四面体的四个面的中心为顶点的四面体与原四面体的体积之比为$\frac{1}{27}$．

Answer 1

分析 由题意画出图形，结合三角形中位线、三角形重心的性质及相似三角形的面积比等于相似比的平方得答案．

解答 解：如图，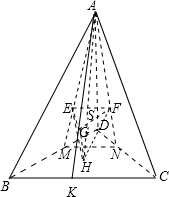

设正四面体ABCD四个面的中心分别为E、F、G、H，
AH为四面体ABCD的面BCD上的高，交面EFG于H，
则$\frac{EF}{MN}=\frac{2}{3}$，又$\frac{MN}{BC}=\frac{1}{2}$，
∴$\frac{EF}{BC}=\frac{1}{3}$，则$\frac{{S}_{△EFG}}{{S}_{△BCD}}=\frac{1}{9}$，
同理可得$\frac{SH}{AH}=\frac{1}{3}$，
∴正四面体的四个面的中心为顶点的四面体与原四面体的体积之比为$\frac{1}{27}$．
故答案为：$\frac{1}{27}$．

点评 本题考查了棱柱、棱锥、棱台的体积，考查了学生的空间想象能力和思维能力，属中档题．