
分析 (1)将椭圆方程化为标准方程,由题意可得a,可得b,即可得到椭圆方程,再由离心率公式计算即可得到所求值;
(2)设AP中点为D,由|BA|=||BP|,所以BD⊥AP,求得AP的斜率,进而得到BD的斜率和中点,可得直线BD的方程,即有B的坐标,求得四边形OPAB的面积为S=S△OAP+S△OMB,化简整理,运用基本不等式即可得到最小值.
解答 解:(1)由题意知椭圆C:$\frac{x^2}{{\frac{1}{m}}}+\frac{y^2}{{\frac{1}{3m}}}=1$,
所以${a^2}=\frac{1}{m}$,${b^2}=\frac{1}{3m}$,
故$2a=2\sqrt{\frac{1}{m}}=2\sqrt{6}$,解得$m=\frac{1}{6}$,
所以椭圆C的方程为$\frac{x^2}{6}+\frac{y^2}{2}=1$.
因为$c=\sqrt{{a^2}-{b^2}}=2$,所以离心率$e=\frac{c}{a}=\frac{{\sqrt{6}}}{3}$.
(2)设线段AP的中点为D.
因为BA=BP,所以BD⊥AP.
由题意知直线BD的斜率存在,
设点P的坐标为(x0,y0)(y0≠0),
则点D的坐标为$(\frac{{{x_0}+3}}{2},\frac{y_0}{2})$,直线AP的斜率${k_{AP}}=\frac{y_0}{{{x_0}-3}}$,
所以直线BD的斜率${k_{BD}}=-\frac{1}{{{k_{AP}}}}=\frac{{3-{x_0}}}{y_0}$,
故直线BD的方程为$y-\frac{y_0}{2}=\frac{{3-{x_0}}}{y_0}(x-\frac{{{x_0}+3}}{2})$.
令x=0,得$y=\frac{x_0^2+y_0^2-9}{{2{y_0}}}$,故$B(0,\frac{x_0^2+y_0^2-9}{{2{y_0}}})$.
由$\frac{x_0^2}{6}+\frac{y_0^2}{2}=1$,得$x_0^2=6-3y_0^2$,化简得$B(0,\frac{-2y_0^2-3}{2y_0^2})$.
因此,S四边形OPAB=S△OAP+S△OAB=$\frac{1}{2}×3×|{y_0}|+\frac{1}{2}×3×|\frac{{-2{y_0}^2-3}}{{2{y_0}}}|$
=$\frac{3}{2}(|{y_0}|+|\frac{{-2{y_0}^2-3}}{{2{y_0}}}|)$=$\frac{3}{2}(2|{y_0}|+\frac{3}{{2|{y_0}|}})$$≥\frac{3}{2}×2\sqrt{2|{y_0}|×\frac{3}{{2|{y_0}|}}}$=$3\sqrt{3}$.
当且仅当$2|{y_0}|=\frac{3}{{2|{y_0}|}}$时,即${y_0}=±\frac{{\sqrt{3}}}{2}∈[-\sqrt{2},\sqrt{2}]$时等号成立.
故四边形OPAB面积的最小值为$3\sqrt{3}$.
点评 本题考查椭圆的方程和离心率的求法,注意运用椭圆的性质和离心率公式,考查四边形面积的最值的求法,注意运用直线的斜率公式和基本不等式,考查化简整理的运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
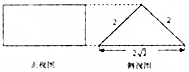
| A. | 8 | B. | 4$\sqrt{2}$ | C. | 16 | D. | $\frac{16}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
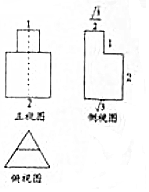 已知一个几何体的三视图如图所示(正视图是两个正方形,俯视图是两个正三角形),则其体积为( )
已知一个几何体的三视图如图所示(正视图是两个正方形,俯视图是两个正三角形),则其体积为( )| A. | $\frac{{3\sqrt{3}}}{2}$ | B. | $\frac{{9\sqrt{3}}}{4}$ | C. | $3\sqrt{3}$ | D. | $\frac{{9\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com