Question

17．在直角坐标系中，如果不同两点A（a，b），B（-a，-b）都在函数y=h（x）的图象上，那么称[A，B]为函数h（x）的一组“友好点”（[A，B]与[B，A]看作一组）．已知定义在[0，+∞）上的函数f（x）满足f（x+2）=$\sqrt{2}$f（x），且当x∈[0，2]时，f（x）=sin$\frac{π}{2}$x．则函数g（x）=$\left\{\begin{array}{l}{f（x），0＜x≤8}\\{-\sqrt{-x}，-8≤x＜0}\end{array}\right.$的“友好点”的组数为（　　）

• A． 4
• B． 5
• C． 6
• D． 7

Answer 1

分析 根据“友好点对”的定义可知，只需要利用图象，作出函数f（x）=-$\sqrt{-x}$，-8≤x＜0关于原点对称的图象，利用对称图象在0＜x≤8上两个图象的交点个数，即为“友好点”的个数．

解答 解：由题意知函数f（x）=-$\sqrt{-x}$，-8≤x＜0关于原点对称的图象为-y=-$\sqrt{x}$，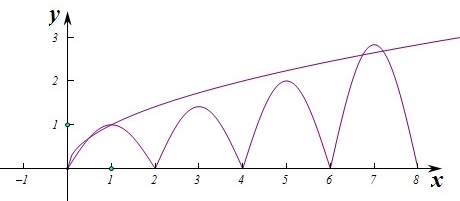
即y=$\sqrt{x}$，0＜x≤8，
在0＜x≤8上作出两个函数的图象如图，
由图象可知两个函数在0＜x≤8上的交点个数有4个，
∴函数f（x）的“友好点”有4个，
故选：A．

点评 本题主要考查新定义题目，弄清本质含义，转化为图象交点是关键，利用数形结合的思想是解决本题的关键