
【题目】如图,在三棱锥![]() 中,△ABC是等边三角形,AB⊥AD,CB⊥CD,点P是AC的中点,记△BPD、△ABD的面积分别为
中,△ABC是等边三角形,AB⊥AD,CB⊥CD,点P是AC的中点,记△BPD、△ABD的面积分别为![]() ,
,![]() ,二面角A-BD-C的大小为
,二面角A-BD-C的大小为![]() ,
,
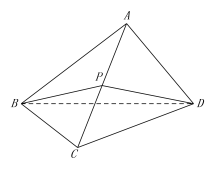
证明:(Ⅰ)平面ACD![]() 平面BDP;
平面BDP;
(Ⅱ)![]() .
.
【答案】(Ⅰ)见解析(Ⅱ)见解析
【解析】
(Ⅰ)由题意可知Rt△BAD≌Rt△BCD,∴AD=CD,又P是AC的中点,∴PB⊥AC,PD⊥AC,可得AC⊥平面BDP ,结合面面垂直的判定定理即可得证。
(Ⅱ)作AM⊥ BD,M为垂足,连接PM,CM.可得AC⊥PM,AC⊥BD,所以BD⊥CM,则∠AMC就是二面角A-BD-C的平面角,即∠AMC=![]() . 可求出
. 可求出![]() 与
与![]() 的关系,即可得证。
的关系,即可得证。
(Ⅰ)证明:∵△ABC是等边三角形,AB⊥AD,CB⊥CD,
∴Rt△BAD≌Rt△BCD,∴AD=CD.
∵点P是AC的中点,∴PB⊥AC,PD⊥AC,
又![]() =P,
=P,![]() 平面BDP,
平面BDP,![]() 平面BDP,
平面BDP,
∴AC⊥平面BDP,
∵![]() 平面ACD,∴平面ACD⊥平面BDP.
平面ACD,∴平面ACD⊥平面BDP.
(Ⅱ)证明:作AM⊥ BD,M为垂足,连接PM,CM.
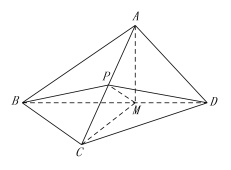
由(1)知AC⊥平面BDP,则AC⊥PM,AC⊥BD,
∵![]() ,∴BD⊥平面ACM,
,∴BD⊥平面ACM,
∴BD⊥CM,则∠AMC就是二面角A-BD-C的平面角,即∠AMC=![]() .
.
又P为AC的中点,PM⊥AC,则∠AMP=![]() ,
,
所以 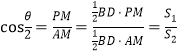 ,
,
所以![]() .
.


科目:高中数学 来源: 题型:
【题目】已知数列![]() .如果数列
.如果数列![]() 满足
满足![]() ,
, ![]() ,其中
,其中![]() ,则称
,则称![]() 为
为![]() 的“陪伴数列”.
的“陪伴数列”.
(Ⅰ)写出数列![]() 的“陪伴数列”
的“陪伴数列”![]() ;
;
(Ⅱ)若![]() 的“陪伴数列”是
的“陪伴数列”是![]() .试证明:
.试证明: ![]() 成等差数列.
成等差数列.
(Ⅲ)若![]() 为偶数,且
为偶数,且![]() 的“陪伴数列”是
的“陪伴数列”是![]() ,证明:
,证明: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的方程是:
的方程是: ![]() ,以坐标原点为极点,
,以坐标原点为极点, ![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)设过原点的直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
, ![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的左右焦点分别
的左右焦点分别![]()
![]() ,过
,过![]() 作垂直于
作垂直于![]() 轴的直线
轴的直线![]() 交椭圆于
交椭圆于![]() 两点,满足
两点,满足![]() .
.
(1)求椭圆![]() 的离心率.
的离心率.
(2)![]() 是椭圆
是椭圆![]() 短轴的两个端点,设点
短轴的两个端点,设点![]() 是椭圆
是椭圆![]() 上一点(异于椭圆
上一点(异于椭圆![]() 的顶点),直线
的顶点),直线![]() 分别与
分别与![]() 轴相交于
轴相交于![]() 两点,
两点,![]() 为坐标原点,若
为坐标原点,若![]() ,求椭圆
,求椭圆![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如下:
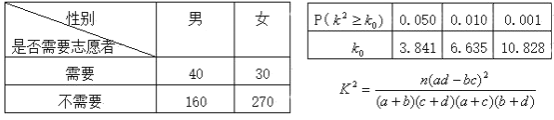
(1)估计该地区老年人中,需要志愿者提供帮助的老年人的比例;
(2)能否有99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(0,-2),椭圆E: ![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,F是椭圆E的右焦点,直线AF的斜率为
,F是椭圆E的右焦点,直线AF的斜率为![]() ,O为坐标原点.
,O为坐标原点.
(1)求E的方程;
(2)设过点A的动直线l与E相交于P,Q两点.当△OPQ的面积最大时,求l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知中心在原点,焦点在![]() 轴上的椭圆
轴上的椭圆![]() 的离心率为
的离心率为![]() ,且经过点
,且经过点![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)是否存在过点![]() 的直线
的直线![]() 与
与![]() 相交于不同的两点
相交于不同的两点![]() ,满足
,满足![]() ?
?
若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 都是各项不为零的数列,且满足
都是各项不为零的数列,且满足![]() ,
,![]() ,其中
,其中![]() 是数列
是数列![]() 的前
的前![]() 项和,
项和,![]() 是公差为
是公差为![]() 的等差数列.
的等差数列.
(1)若数列![]() 的通项公式分别为
的通项公式分别为![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(2)若![]() (
(![]() 是不为零的常数),求证:数列
是不为零的常数),求证:数列![]() 是等差数列;
是等差数列;
(3)若![]() (
(![]() 为常数,
为常数,![]() ),
),![]() (
(![]() ,
,![]() ),对任意
),对任意![]() ,
,![]() ,求出数列
,求出数列![]() 的最大项(用含
的最大项(用含![]() 式子表达).
式子表达).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校艺术节对同一类的![]() ,
,![]() ,
,![]() ,
,![]() 四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
甲说:“是![]() 或
或![]() 作品获得一等奖”;
作品获得一等奖”;
乙说:“![]() 作品获得一等奖”;
作品获得一等奖”;
丙说:“![]() ,
,![]() 两项作品未获得一等奖”;
两项作品未获得一等奖”;
丁说:“是![]() 作品获得一等奖”.
作品获得一等奖”.
若这四位同学中只有两位说的话是对的,则获得一等奖的作品是__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com