Question

7．已知函数$f（x）=\left\{\begin{array}{l}{2^x}，x≤0\\{x^2}，x＞0\end{array}\right.$，若函数g（x）=f（x）-k（x-1）恰有两个零点，则实数k的取值范围是（　　）

• A． （-∞，-1）∪（4，+∞）
• B． （-∞，-1]∪[4，+∞）
• C． [-1，0）∪（4，+∞）
• D． [-1，0）∪[4，+∞）

Answer 1

分析 问题转化为函数f（x）和y=k（x-1）的图象有2个交点，结合图象求出k的范围即可．

解答 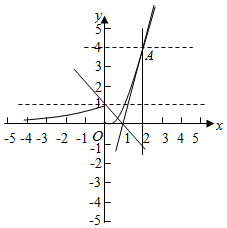解：若函数g（x）=f（x）-k（x-1）恰有两个零点，
则f（x）与y=k（x-1）有2个交点，
画出函数f（x）和y=k（x-1）的图象，如图所示：
，
对于y=k（x-1）显然直线过定点（1，0），
①k＜0时，k=-1时，直线和f（x）有2个交点，
绕着（1，0）旋转直线得k∈[-1，0），
②k＞0时，设y=k（x-1）与f（x）相切时，切点为A（x₀，y₀），
则$\left\{\begin{array}{l}{f′{（x}_{0}）={2x}_{0}}\\{{{{y}_{0}=x}_{0}}^{2}}\\{{y}_{0}={2x}_{0}{（x}_{0}-1）}\end{array}\right.$，解得：$\left\{\begin{array}{l}{{x}_{0}=2}\\{{y}_{0}=4}\\{k=4}\end{array}\right.$，
此时直线的斜率是4，当k＞4时，直线和f（x）相割，有2个交点，
综上，k∈[-1，0）∪（4，+∞），
故选：C．

点评 本题考查了函数的零点问题，考查指数函数、二次函数的性质，考查转化思想以及数形结合思想，是一道中档题．