
分析 ①每次1球,摸取3次,则恰有两次红球的概率=$\frac{{∁}_{3}^{2}{∁}_{3}^{1}}{{∁}_{6}^{3}}$.
②设摸到红球次数为X,则X的取值分别为0,1,2,3,P(X=k)=$\frac{{∁}_{3}^{k}{∁}_{3}^{3-k}}{{∁}_{6}^{3}}$,(k=0,1,2,3).
解答 解:①每次1球,摸取3次,则恰有两次红球的概率P=$\frac{{∁}_{3}^{2}{∁}_{3}^{1}}{{∁}_{6}^{3}}$=$\frac{3×3}{\frac{6×5×4}{1×2×3}}$=$\frac{9}{20}$.
②设摸到红球次数为X,则X的可能取值为0,1,2,3,P(X=k)=$\frac{{∁}_{3}^{k}{∁}_{3}^{3-k}}{{∁}_{6}^{3}}$,(k=0,1,2,3).
∴P(X=0)=$\frac{1}{20}$,P(X=1)=$\frac{9}{20}$,P(X=2)=$\frac{9}{20}$,P(X=3)=$\frac{1}{20}$,
∴E(X)=0+1×$\frac{9}{20}$+2×$\frac{9}{20}$+3×$\frac{1}{20}$=$\frac{3}{2}$.
故答案为:$\frac{9}{20},\frac{3}{2}$.
点评 本题考查了超几何分布列的概率计算公式及其数学期望,考查了推理能力与计算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{17}{2}$ | B. | 9 | C. | $\frac{29}{3}$ | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{8}{9}$ | C. | $\frac{20}{9}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
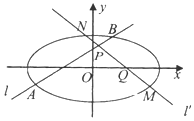 已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$,过$P({0,\frac{b}{2}})$的直线l与椭圆交于A,B两点,过Q(x0,0)(|x0|<a)的直线l'与椭圆交于M,N两点.
已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$,过$P({0,\frac{b}{2}})$的直线l与椭圆交于A,B两点,过Q(x0,0)(|x0|<a)的直线l'与椭圆交于M,N两点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | -2 | C. | -1 | D. | 0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com