
分析 (1)运用“零点分段法”解不等式|3x+1|+|3x-3|≥8,分成三段求解,再综合;
(2)运用绝对值三角不等式和基本不等式求参数m的取值范围.
解答 解:(1)当a=1时,f(x)=|3x+1|+|3x-3|,
采用“零点分段法”解不等式|3x+1|+|3x-3|≥8如下:
①当x≥1时,3x+1+3x-3≥8,解得,x≥$\frac{5}{3}$;
②当-$\frac{1}{3}$≤x<1时,3x+1-3x+3≥8,不等式无解;
③当x<-$\frac{1}{3}$时,-3x-1-3x+3≥8,解得,x≤-1,
综合以上讨论得,原不等式的解集为:(-∞,-1]∪[$\frac{5}{3}$,+∞);
(2)∵不等式f(x)≥m恒成立,∴f(x)min≥m,
根据绝对值三角不等式得,|3x+$\frac{1}{a}$|+|3x-3a|≥|$\frac{1}{a}$+3a|,
即f(x)min=|$\frac{1}{a}$+3a|,且a>0,
所以,$\frac{1}{a}$+3a≥m,
根据基本不等式,$\frac{1}{a}$+3a≥2$\sqrt{3}$,
所以,m≤2$\sqrt{3}$,
即实数m的取值范围为:(-∞,2$\sqrt{3}$].
点评 本题主要考查了绝对值不等式的解法,涉及零点分段法,以及含绝对值的不等式恒成立问题的解法,用到绝对值三角不等式和基本不等式,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y2=4x | B. | x2=-4y | C. | x2+4y2=1 | D. | x2-4y2=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
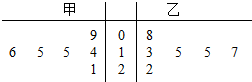
| A. | ${\overline{x}}_{1}$>${\overline{x}}_{2}$,s${\;}_{1}^{2}$<${s}_{2}^{2}$ | B. | ${\overline{x}}_{1}$=${\overline{x}}_{2}$,s${\;}_{1}^{2}$>${s}_{2}^{2}$ | ||
| C. | ${\overline{x}}_{1}$=${\overline{x}}_{2}$,s${\;}_{1}^{2}$=${s}_{2}^{2}$ | D. | ${\overline{x}}_{1}$=${\overline{x}}_{2}$,s${\;}_{1}^{2}$<${s}_{2}^{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com