
| A. | (0,$\frac{1}{2}$)∪($\frac{3}{4}$,+∞) | B. | (-∞,$\frac{1}{2}$)∪($\frac{3}{4}$,+∞) | C. | ($\frac{1}{2}$,+∞) | D. | (-∞,$\frac{1}{2}$) |
分析 函数满足f(-x)=f(x)=f(|x|),故函数f(x)为偶函数,且在(0,+∞)单调递增,把f(3a-2)>f(a-1),转化为|3a-2|>|a-1|,即8a2-10a+3>0,求解即得到实数a的取值范围.
解答 解:∵函数f(x)=e|x|+x2(e为自然对数的底数),
∴f(-x)=f(x),故函数f(x)为偶函数⇒f(x)=f(|x|),且在(0,+∞)单调递增,
∵f(3a-2)>f(a-1),∴|3a-2|>|a-1|,
即8a2-10a+3>0,解得$a<\frac{1}{2}或a>\frac{3}{4}$,实数a的取值范围为:(-∞,$\frac{1}{2}$)∪($\frac{3}{4}$,+∞).
故选:B
点评 本题考察了偶函数的性质,单调性,解函数不等式的基本方法,属于中档题


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 数学 | 95 | 75 | 80 | 94 | 92 | 65 | 67 | 84 | 98 | 71 | 67 | 93 | 64 | 78 | 77 | 90 | 57 | 92 | 72 | 93 |
| 物理 | 90 | 63 | 72 | 92 | 91 | 71 | 58 | 91 | 93 | 81 | 77 | 82 | 48 | 91 | 69 | 96 | 61 | 84 | 78 | 93 |
 | 优秀 | 不优秀 | 合计 |
| 优秀 | 6 | 2 | 8 |
| 不优秀 | 2 | 10 | 12 |
| 合计 | 8 | 12 | 20 |
| P(K2≥k0) | 0.1 | 0.05 | 0.01 | 0.005 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
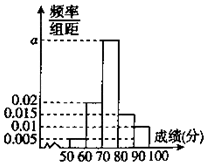 为了了解某学校高二年级学生的物理成绩,从中抽取n名学生的物理成绩(百分制)作为样本,按成绩分成 5组:[50,60),[60,70),[70,80),[80,90),[90,100],频率分布直方图如图所示,成绩落在[70,80)中的人数为20.
为了了解某学校高二年级学生的物理成绩,从中抽取n名学生的物理成绩(百分制)作为样本,按成绩分成 5组:[50,60),[60,70),[70,80),[80,90),[90,100],频率分布直方图如图所示,成绩落在[70,80)中的人数为20.| P(K2≥k) | 0.50 | 0.05 | 0.025 | 0.005 |
| k | 0.455 | 3.841 | 5.024 | 7.879 |
| 男生 | 女生 | 合计 | |
| 优秀 | |||
| 不优秀 | |||
| 合计 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,2} | B. | {2,3} | C. | {1,2,3} | D. | {2,3,4} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com