
分析 ( I)先化简函数,再求函数f(x)的单调增区间以及对称中心;
( II)求出g(x),利用函数g(x)的图象关于y轴对称,求实数m的最小值.
解答 解:( I)∵f(x)=$\sqrt{3}$sin2x-2sin2x+2=$\sqrt{3}$sin2x+cos2x+1=2sin(2x+$\frac{π}{6}$)+1 …(2分)
∴令-$\frac{π}{2}$+2kπ≤2x+$\frac{π}{6}$≤$\frac{π}{2}$+2kπ,
∴-$\frac{π}{3}$+kπ≤x≤$\frac{π}{6}$+kπ,
∴函数的单调增区间为[-$\frac{π}{3}$+kπ,$\frac{π}{6}$+kπ],k∈Z …(4分)
又令$2x+\frac{π}{6}=kπ,k∈Z$,解得$x=\frac{kπ}{2}-\frac{π}{12},k∈Z$
∴函数的对称中心为$(\frac{kπ}{2}-\frac{π}{12},1),k∈Z$…(6分)
( II)若函数f(x)的图象向左平移m(m>0)个单位,则得到的函数为$g(x)=2sin[2(x+m)+\frac{π}{6}]+1$
∴$g(x)=2sin(2x+2m+\frac{π}{6})+1$…(8分)
又函数g(x)的图象关于y轴对称
∴当x=0时,函数g(x)取得最大或最小值
∴$2m+\frac{π}{6}=kπ+\frac{π}{2},k∈Z$
∴$m=\frac{kπ}{2}+\frac{π}{6},k∈Z$…(10分)
又m>0
∴实数m的最小值为$\frac{π}{6}$.…(12分)
点评 本题考查三角函数的图象与性质,考查三角函数的化简,属于中档题.


科目:高中数学 来源: 题型:解答题
| 投放量x | 6 | 8 | 10 | 12 |
| 销售量y | 2 | 3 | 5 | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{1}{2}$)∪($\frac{3}{4}$,+∞) | B. | (-∞,$\frac{1}{2}$)∪($\frac{3}{4}$,+∞) | C. | ($\frac{1}{2}$,+∞) | D. | (-∞,$\frac{1}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,正四棱锥P-ABCD中底面边长为2$\sqrt{2}$,侧棱PA与底面ABCD所成角的正切值为$\frac{{\sqrt{6}}}{2}$.
如图,正四棱锥P-ABCD中底面边长为2$\sqrt{2}$,侧棱PA与底面ABCD所成角的正切值为$\frac{{\sqrt{6}}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a${\;}^{\frac{3}{2}}$ | B. | a${\;}^{\frac{1}{6}}$ | C. | a${\;}^{\frac{5}{6}}$ | D. | a${\;}^{\frac{6}{5}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
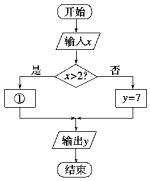 某市的出租车收费办法如下:
某市的出租车收费办法如下:| A. | y=7+2.5x | B. | y=8+2.5x | C. | y=2+2.5x | D. | y=3+2.5x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0或6 | B. | 0或$\frac{1}{6}$ | C. | 6或 $\frac{1}{6}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com