
分析 (Ⅰ)利用绝对值不等式的几何意义推出|3a+b|+|a-b|≥4|a|,转化所求解不等式为|x+1|+|x-1|≤4,推出结果即可.
(Ⅱ)利用作差法,结合已知条件推出结果即可.
解答 (Ⅰ)解:|3a+b|+|a-b|≥|3a+b+a-b|=4|a|,当且仅当(3a+b)(a-b)≥0时取等号,
只需:4|a|≥|a|(|x+1|+|x-1|),由于a≠0,只需|x+1|+|x-1|≤4,表示数轴上的点与-1,1的距离之和小于等于4,
所以:x的取值范围为:[-2,2];
(Ⅱ)解得:M=(0,1),a∈M,b∈M知:$\frac{1}{ab}+1-\frac{1}{a}-\frac{1}{b}=\frac{ab+1-a-b}{ab}=\frac{(a-1)(b-1)}{ab}$>0,
即$\frac{1}{ab}+1>\frac{1}{a}+\frac{1}{b}$.
点评 本题考查绝对值不等式的几何意义,不等式的解法,函数恒成立条件的应用,考查转化思想以及计算能力.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{13}$ | B. | -$\frac{1}{13}$ | C. | $\frac{1}{11}$ | D. | -$\frac{1}{11}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[-\frac{1}{e},e]$ | B. | $[-\frac{2}{e},2e]$ | C. | $[-\frac{3}{e},3e]$ | D. | $(-\frac{2}{e},2e)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 22 | B. | 16 | C. | 12 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
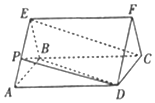 如图,三棱柱ABE-DCF中,△EAB是正三角形,四边形ABCD是矩形,且EA=2,BC=2$\sqrt{3}$,EC=4.
如图,三棱柱ABE-DCF中,△EAB是正三角形,四边形ABCD是矩形,且EA=2,BC=2$\sqrt{3}$,EC=4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com