
| A. | ② | B. | ①② | C. | ①③ | D. | ①②③ |
分析 根据函数解析式分析器奇偶性和最值等,得到正确选项.
解答 解:由已知解析式得到函数定义域为R,
对于①,f(-x)=$\frac{-x}{(-x)^{2}+a}=-\frac{x}{{x}^{2}+a}$=-f(x);所以为奇函数;故①正确;
对于②,a>0时,f(x)=$\frac{1}{x+\frac{a}{x}}≤\frac{1}{2\sqrt{a}}=\frac{\sqrt{a}}{2a}$,当且仅当x=$\frac{a}{x}$时等号成立;故②正确;
对于③,只有a≠0时,函数图象经过坐标原点(0,0),故③错误;
故选B.
点评 本题考查了函数奇偶性的判断、最值求法等;将解析式适当变形是关键.


科目:高中数学 来源: 题型:选择题
| A. | (0,2) | B. | (1,+∞) | C. | (0,1) | D. | (1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
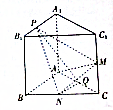 如图,已知有直三棱柱ABC-A1B1C1中,AA1=AB=AC=1,AB⊥AC,M、N、Q分别是CC1、BC、AC的中点,点P在线段A1B1上运动.
如图,已知有直三棱柱ABC-A1B1C1中,AA1=AB=AC=1,AB⊥AC,M、N、Q分别是CC1、BC、AC的中点,点P在线段A1B1上运动.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4x-y+4=0 | B. | 4x-y-4=0 | C. | 4x+y+4=0 | D. | 4x+y-4=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2e-2}$ | B. | $\frac{e-2}{2e-2}$ | C. | $\frac{3-e}{4e-4}$ | D. | $\frac{e}{2e-2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{24}$ | B. | $\frac{1}{12}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com