
分析 (1)利用倍角公式及两角差的正弦函数公式化简可得解析式:f(x)=sin(2x-$\frac{π}{6}$)-1,利用周期公式即可得解;
(2)由$x∈({0,\frac{π}{2}})$,可得2x-$\frac{π}{6}$∈(-$\frac{π}{6}$,$\frac{5π}{6}$),利用正弦函数的图象和性质即可求得其值域.
解答 解:(1)∵$f(x)=\sqrt{3}sinxcosx-{cos^2}x-\frac{1}{2},x∈R$.
=$\frac{\sqrt{3}}{2}$sin2x-$\frac{cos2x+1}{2}$-$\frac{1}{2}$
=sin(2x-$\frac{π}{6}$)-1,
∴T=$\frac{2π}{2}=π$.
(2)∵$x∈({0,\frac{π}{2}})$,
∴2x-$\frac{π}{6}$∈(-$\frac{π}{6}$,$\frac{5π}{6}$),
∴sin(2x-$\frac{π}{6}$)∈(-$\frac{1}{2}$,1],
∴f(x)∈(-$\frac{3}{2}$,0].
点评 本题主要考查了倍角公式及两角差的正弦函数公式,周期公式,正弦函数的图象和性质的综合应用,考查了计算能力,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
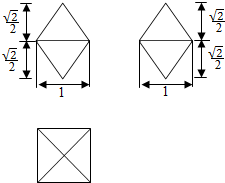
| A. | $\frac{{\sqrt{2}}}{3}π$? | B. | $\sqrt{2}π$? | C. | 2π? | D. | $\frac{{2\sqrt{2}}}{3}π$? |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
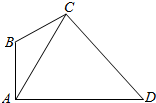 在如图所示的四边形ABCD中,已知AB⊥AD,∠ABC=120°,∠ACD=60°,AD=2$\sqrt{3}$,设∠ACB=θ,点C到AD的距离为h.
在如图所示的四边形ABCD中,已知AB⊥AD,∠ABC=120°,∠ACD=60°,AD=2$\sqrt{3}$,设∠ACB=θ,点C到AD的距离为h.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com