
| A. | 14 | B. | 15 | C. | 16 | D. | 17 |
分析 设4x+y=t,代入条件可得4xy=$\frac{4t}{17-t}$,(0<t<17),将4x,y可看作二次方程m2-tm+$\frac{4t}{17-t}$=0的两根,由△≥0,
运用二次不等式的解法即可得到所求最值,进而得到它们的差.
解答 解:设4x+y=t,
4x+$\frac{1}{x}$+y+$\frac{4}{y}$=17,即为(4x+y)+$\frac{4x+y}{xy}$=17,
即有t+$\frac{t}{xy}$=17,
可得xy=$\frac{t}{17-t}$,即4xy=$\frac{4t}{17-t}$,(0<t<17),
即有4x,y可看作二次方程m2-tm+$\frac{4t}{17-t}$=0的两根,
由△≥0,可得t2-$\frac{16t}{17-t}$≥0,
化为t2-17t+16≤0,
解得1≤t≤16,
当x=$\frac{1}{8}$,y=$\frac{1}{2}$时,函数F(x,y)取得最小值1;
当x=2,y=8时,函数F(x,y)取得最大值16.
可得函数F(x,y)=4x+y的最大值与最小值的差为15.
故选:B.
点评 本题考查函数的最值的求法,注意运用换元法和二次方程的实根的分布,考查判别式法和二次不等式的解法,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | [-4,$\frac{7}{16}$] | B. | [-4,1] | C. | [$\frac{1}{4}$,$\frac{7}{16}$] | D. | [$\frac{1}{4}$,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
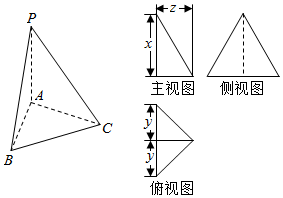 如图,已知三棱锥P-ABC的底面是等腰直角三角形,且∠ACB=$\frac{π}{2}$,侧面PAB⊥底面ABC,AB=PA=PB=2.则这个三棱锥的三视图中标注的尺寸x,y,z分别是( )
如图,已知三棱锥P-ABC的底面是等腰直角三角形,且∠ACB=$\frac{π}{2}$,侧面PAB⊥底面ABC,AB=PA=PB=2.则这个三棱锥的三视图中标注的尺寸x,y,z分别是( )| A. | $\sqrt{3}$,1,$\sqrt{2}$ | B. | $\sqrt{3}$,1,1 | C. | 2,1,$\sqrt{2}$ | D. | 2,1,1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
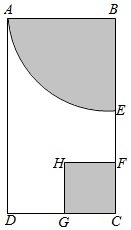 如图,矩形ABCD中,AB=2,BC=4,点E、G分别为BC、DC中点,点F为EC中点,则矩形去掉阴影部分后,以BC为轴旋转一周所得的几何体的体积是$\frac{29π}{3}$.
如图,矩形ABCD中,AB=2,BC=4,点E、G分别为BC、DC中点,点F为EC中点,则矩形去掉阴影部分后,以BC为轴旋转一周所得的几何体的体积是$\frac{29π}{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com