
已知抛物线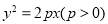 上的任意一点
上的任意一点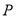 到该抛物线焦点的距离比该点到
到该抛物线焦点的距离比该点到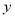 轴的距离多1.
轴的距离多1.
(1)求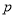 的值;
的值;
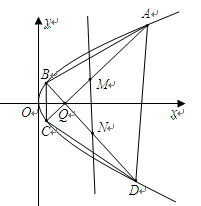
(2)如图所示,过定点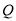 (2,0)且互相垂直的两条直线
(2,0)且互相垂直的两条直线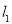 、
、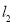 分别与该抛物线分别交于
分别与该抛物线分别交于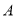 、
、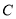 、
、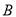 、
、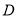 四点.
四点.
(i)求四边形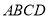 面积的最小值;
面积的最小值;
(ii)设线段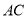 、
、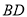 的中点分别为
的中点分别为 、
、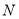 两点,试问:直线
两点,试问:直线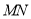 是否过定点?若是,求出定点坐标;若不是,请说明理由.
是否过定点?若是,求出定点坐标;若不是,请说明理由.
(1)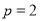 (2)(i)四边形
(2)(i)四边形 面积的最小值是48(ii)
面积的最小值是48(ii)
【解析】
试题分析:(1)直接利用抛物线的定义
(2)(i)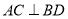 S四边形ABCD,
S四边形ABCD,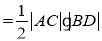 ,利用弦长
,利用弦长
公式,以及基本不等式,二次函数在闭区间上的最值问题
的解法求解
(ii)恒过定点问题的常规解法
试题解析:
(1)由已知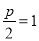 ∴
∴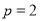
(2)(i)由题意可设直线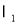 的方程为
的方程为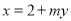 (
(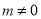 ),代入
),代入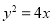 得
得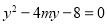
设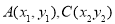 则
则 ,
,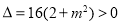
∴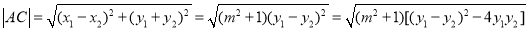
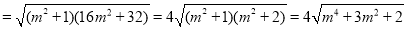 6分
6分
同理可得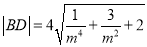 7分
7分
S四边形ABCD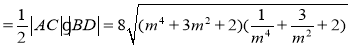
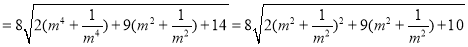 8分
8分
设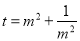 则
则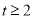 ∴S四边形ABCD
∴S四边形ABCD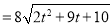
∵函数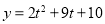 在
在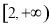 上是增函数
上是增函数
∴S四边形ABCD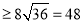 ,当且仅当即
,当且仅当即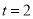 即
即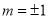 时取等号
时取等号
∴四边形 面积的最小值是48. 9分
面积的最小值是48. 9分
(ii)由①得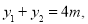 ∴
∴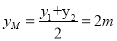 ∴
∴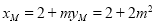
∴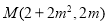 , 11分
, 11分
同理得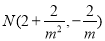 12分
12分
∴直线的方程可表示为
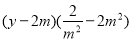
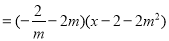
即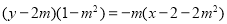
当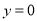 时得
时得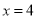
∴直线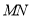 过定点(4,0). 14分
过定点(4,0). 14分
注:第(2)中的第(i)问:
S四边形ABCD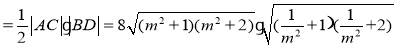
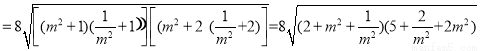
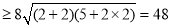 (当且仅当
(当且仅当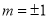 时取等号)也可.
时取等号)也可.
考点:本题主要考查抛物线标准方程,简单几何性质,直线与抛物线的位置关系,弦长公式,基本不等式,二次函数在闭区间上的最值问题等基础知识.考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2015届苏教版选修2-3高二数学双基达标1.4练习卷(解析版) 题型:填空题
甲、乙两人从4门课程中各选修2门,则甲、乙所选的课程中至少有1门不相同的选法共有________.
查看答案和解析>>
科目:高中数学 来源:2015届苏教版选修2-3高二数学双基达标1.1练习卷(解析版) 题型:解答题
某班新年联欢晚会原定的5个节目已排成节目单,开演前又增加了两个新节目,如果将这2个节目插入原节目单中,那么有多少种不同的插法?
查看答案和解析>>
科目:高中数学 来源:2015届苏教版选修2-3高二数学双基达标1.1练习卷(解析版) 题型:解答题
已知集合M={-3,-2,-1,0,1,2},P(a,b)表示平面上的点(a,b∈M),问:
(1)P可表示平面上多少个不同的点?
(2)P可表示平面上多少个第二象限的点?
(3)P可表示多少个不在直线y=x上的点?
查看答案和解析>>
科目:高中数学 来源:2015届福建省龙岩市高二上学期教学质量检查理科数学试卷(解析版) 题型:解答题
已知在锐角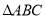 中,内角
中,内角 所对的边分别是
所对的边分别是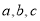 ,且
,且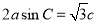 .
.
(1)求角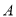 的大小;
的大小;
(2)若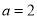 ,
,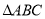 的面积等于
的面积等于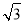 ,求
,求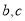 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源:2015届福建省高二上学期期中考试理科数学试卷(解析版) 题型:填空题
已知命题p: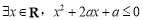 ,则命题p的否定是_________________;若命题p为假命题,则实数a的取值范围是_______________.
,则命题p的否定是_________________;若命题p为假命题,则实数a的取值范围是_______________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com