
如图,在三棱柱ABC—A1B1C1中,AA1⊥平面ABC,AB⊥BC,且AB =BC=2,点N为B1C1的中点,点P在棱A1C1上运动.
=BC=2,点N为B1C1的中点,点P在棱A1C1上运动.
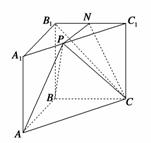
(1)试问点P在何处时,AB∥平面PNC,并证明你的结论;
(2)在(1)的条件下,若AA1<AB,直线B1C与平面BCP所成角的正弦值为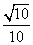 ,求二面角A-BP-C的大小.
,求二面角A-BP-C的大小.
(1)当点P为A1C1的中点时,AB∥平面PNC.
∵P为A1C1的中点,N为B1C1的中点,∴PN∥A1B1∥AB
∵AB⊄平面PNC,PN⊂平面PNC,∴AB∥平面PNC.
(2)设AA1=m,则m<2,∵AB、BC、BB,两两垂直,
∴以B为原点,BA、BC,BB1为x轴、y轴,z轴建立空间直角坐标系,则A(2,0,0),C(0,2,0),B1(0,0,m),A1(2,0,m),C1(0,2,m),
∴P(1,1,m),设平面BCP的法向量n=(x,y,z),
则由n·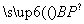 =0,n·
=0,n·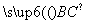 =0,解得y=0,x=-mz,
=0,解得y=0,x=-mz,
令z=0,则n=(-m,0,-1),又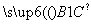 =(0,2,-m),
=(0,2,-m),
直线B1C与平面BCP所成角正弦值为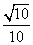 ,
,
∴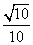 =
=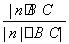 ,解之得m=1
,解之得m=1
∴n=(-1,0,1)
易求得平面ABP的法向量n1=(0,-1,1)
cosα=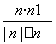 =
= ,设二面角的平面角为θ,则cosθ=-
,设二面角的平面角为θ,则cosθ=- ,∴θ=120°.
,∴θ=120°.


 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:
在下列结论中,正确的是( )
①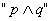 为真是
为真是 为真的充分不必要条件
为真的充分不必要条件
②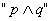 为假是
为假是 为真的充分不必要条件
为真的充分不必要条件
③ 为真是
为真是 为假的必要不充分条件
为假的必要不充分条件
④ 为真是
为真是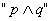 为假的必要不充分条件
为假的必要不充分条件
A.①② B.①③ C.②④ D.③④
查看答案和解析>>
科目:高中数学 来源: 题型:
当x∈R,|x|< 1时,有如下表达式:
1时,有如下表达式:
1+x+x2+…+xn+…=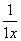 ,
,
两边同时积分得:∫ 01dx+∫
01dx+∫ 0xdx+∫
0xdx+∫ 0x2dx+…+∫
0x2dx+…+∫ 0xndx+…=∫
0xndx+…=∫ 0
0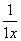 dx,
dx,
从而得到如下等式:
1× +
+ ×(
×( )2+
)2+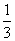 ×(
×( )3+…+
)3+…+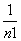 ×(
×( )n+1+…=ln2,
)n+1+…=ln2,
请根据以上材料所蕴含的数学思想方法,计算:
C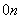 ×
× +
+ C
C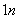 ×(
×( )2+
)2+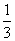 C
C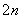 ×(
×( )3+…+
)3+…+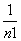 C
C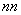 ×(
×( )n+1=________.
)n+1=________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com