
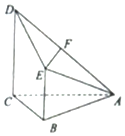
 已知四棱锥A-BCDE中,侧面△ABC为等边三角形,BE=AB,CD=2AB,CD∥BE,且CD⊥平面ABC,F为棱AD的中点.
已知四棱锥A-BCDE中,侧面△ABC为等边三角形,BE=AB,CD=2AB,CD∥BE,且CD⊥平面ABC,F为棱AD的中点.分析 (1)取AC中点G,连接FG,BG,推导出FGBE为平行四边形,从而EF∥BG,由此能证明EF∥面ABC.
(2)推导出BG⊥AG,CD⊥BG,从而BG⊥面ADC,进而EF⊥面ADC,由此能证明面ADE⊥面ADC.
(3)取BC的中点M,连接AM,推导出AM为四棱锥A-BCDE的高,由此能求出四棱锥A-BCDE的体积.
解答 证明:(1)取AC中点G,连接FG,BG,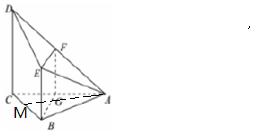
∵F,G分别是AD,AB的中点,
∴FG∥CD,且$FG=\frac{1}{2}CD$,
∵BE∥CD,∴FG与BE平行且相等,∴FGBE为平行四边形,
∴EF∥BG.又EF?面ABC,BG?面ABC,
∴EF∥面ABC.
(2)∵△ABC为等边三角形,∴BG⊥AG,
又∵CD⊥面ABC,BG?面ABC,∴CD⊥BG,
∴BG垂直于面ADC的两条相交直线AC,CD,
∴BG⊥面ADC,∵EF∥BG,∴EF⊥面ADC,
∵EF?面ADE,∴面ADE⊥面ADC.
解:(3)取BC的中点M,连接AM,
∵△ABC为等边三角形,∴AM⊥BC,
又AM⊥CD,AM⊥平面BCDE,故AM为四棱锥A-BCDE的高,
∵AB=a,∴$AM=\frac{{\sqrt{3}}}{2}a$,又${S_{BCDE}}=\frac{a+2a}{2}×a=\frac{3}{2}{a^2}$,
∴${V_{A-BCDE}}=\frac{1}{3}×\frac{3}{2}{a^2}×\frac{{\sqrt{3}}}{2}a=\frac{{\sqrt{3}}}{4}{a^3}$.
点评 本题考查线面平行、面面垂直的证明,考查四棱锥的体积的求法,考查推理论证能力、运算求解能力、空间想象能力,考查数形结合思想、化归与转化思想,考查创新意识、应用意识,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | 2个 | B. | 4个 | C. | 6个 | D. | 8个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | 3 | D. | -3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
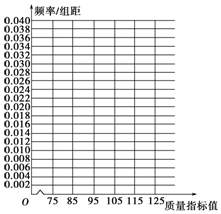 从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量结果得如下频数分布表:
从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量结果得如下频数分布表:| 质量指标值分组 | [75,85) | [85,95) | [95,105) | [105,115) | [115,125) |
| 频数 | 6 | 26 | 38 | 22 | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ②①③ | B. | ③②① | C. | ①②③ | D. | ③①② |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 204 | B. | 240 | C. | 729 | D. | 920 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com