
 从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量结果得如下频数分布表:
从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量结果得如下频数分布表:| 质量指标值分组 | [75,85) | [85,95) | [95,105) | [105,115) | [115,125) |
| 频数 | 6 | 26 | 38 | 22 | 8 |
分析 (1)由已知作出频率分布表,由此能作出作出这些数据的频率分布直方图.
(2)由频率分布直方图能求出质量指标值的样本中位数、平均数及方差.
(3)质量指标值不低于95的产品所占比例的估计值.由于该估计值小于0.8,故不能认为该企业生产的这种产品“质量指标值不低于95 的产品至少要占全部产品80%的规定.
解答 解:(1)由已知作出频率分布表为:
| 质量指标值分组 | [75,85) | [85,95) | [95,105) | [105,115) | [115,125) |
| 频数 | 6 | 26 | 38 | 22 | 8 |
| 频率 | 0.06 | 0.26 | 0.38 | 0.22 | 0.08 |
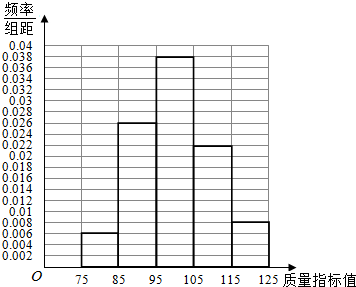
点评 本题考查频率分布直方图的作法,考查平均数、中位数、方差的求法,考查产品质量指标所占比重的估计值的计算与应用,是基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | f(0)=0 | B. | 对?x∈R,f(x)=0都成立 | ||
| C. | ?x0∈R,使得f(x0)+f(-x0)=0 | D. | 对?x∈R,f(x)+f(-x)=0都成立 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
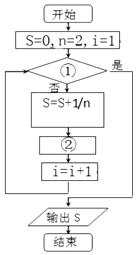
| A. | i<30,n=n+2 | B. | i>30,n=n+2 | C. | i<30,n=n+1 | D. | i>30,n=n+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
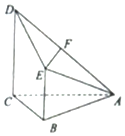 已知四棱锥A-BCDE中,侧面△ABC为等边三角形,BE=AB,CD=2AB,CD∥BE,且CD⊥平面ABC,F为棱AD的中点.
已知四棱锥A-BCDE中,侧面△ABC为等边三角形,BE=AB,CD=2AB,CD∥BE,且CD⊥平面ABC,F为棱AD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{6}{7}$ | B. | $\frac{5}{7}$ | C. | $\frac{3}{7}$ | D. | $\frac{1}{7}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com