练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    7．如图给出了计算S=$\frac{1}{2}$+$\frac{1}{4}$+…+$\frac{1}{60}$的值的程序框图，其中 ①②分别是（　　）
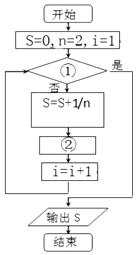
    A．i＜30，n=n+2B．i＞30，n=n+2C．i＜30，n=n+1D．i＞30，n=n+1

    分析 分析要计算计算S=$\frac{1}{2}$+$\frac{1}{4}$+…+$\frac{1}{60}$的值需用“直到型”循环结构，按照程序执行运算．

    解答 解：①的意图是为直到型循环结构构造满足跳出循环的条件，
    分母是从2到60，故条件是i＞30；
    ②的意图为表示各项的分母，
    相邻分母相差2，
    故语句是n=n+2．
    故选：B．

    点评 本题考查程序框图应用，重在解决实际问题，通过把实际问题分析，经判断写出需要填入的内容，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    9．已知a，b∈（0，1）记M=a•b，N=a+b-1则M与N的大小关系是（　　）
    A．M＜NB．M=NC．M＞ND．不确定

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．cos135°的值为（　　）
    A．$\frac{1}{2}$B．$-\frac{1}{2}$C．$\frac{{\sqrt{2}}}{2}$D．$-\frac{{\sqrt{2}}}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．在△ABC中，已知c-b=1，bc=30，S△=$\frac{15}{2}$，求∠A和a．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．函数f（x）=sin（2x+φ），其中φ为实数，若f（x）≤|f（$\frac{π}{6}$）|对（0，+∞）恒成立，且$f（\frac{π}{2}）＞f（π）$，则f（x）的单调递增区间是[$\frac{π}{6}$+kπ，$\frac{2π}{3}$+kπ]，k∈Z．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．设函数$f（x）=sin（2x+\frac{π}{3}）+\sqrt{3}-2\sqrt{3}{cos^2}$x+1
    （1）求f（x）的最小正周期及其图象的对称中心；
    （2）求函数f（x）的单调递增区间．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．射洪县高三教学工作会将在射洪中学召开，学校安排A，B，C，D，E，F六名工作人员分配到繁荣，富强两个校区参与接待工作，若A，B必须同组，且每组至少2人，则不同的分配方法有（　　）
    A．18种B．20种C．22种D．24种

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

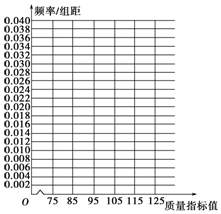    16．从某企业生产的某种产品中抽取100件，测量这些产品的一项质量指标值，由测量结果得如下频数分布表：
    质量指标值分组[75，85）[85，95）[95，105）[105，115）[115，125）
    频数62638228
    （1）作出这些数据的频率分布直方图：
    （2）估计这种产品质量指标值的中位数、平均数及方差（同一组中的数据用该组区间的中点值作代表）（精确到0.01）；
    （3）根据以上抽样调查数据，能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品80%”的规定？

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．对某校小学生进行心理障碍测试，得到如下列联表（单位：名）
    性别与心理障碍列联表
    焦虑说谎懒惰总计
    女生5101530
    男生20105080
    总计2520651110
    试说明三种心理障碍分别与性别的关系如何．（我们规定：如果随机变量K2的观测值小于2.076，就认为没有充分的证据显示“两个分类变量有关系”．参考值图表见题3）

    查看答案和解析>>

    同步练习册答案