练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    19．射洪县高三教学工作会将在射洪中学召开，学校安排A，B，C，D，E，F六名工作人员分配到繁荣，富强两个校区参与接待工作，若A，B必须同组，且每组至少2人，则不同的分配方法有（　　）
    A．18种B．20种C．22种D．24种

    分析 根据题意，按分成2个组的人数分3种情况讨论：①、A，B在一组，C，D，E，F都分在另一组，②、C，D，E，F中取出1人，与A、B一组，剩下3人一组，③、C，D，E，F中取出2人，与A、B一组，剩下2人一组，分别求出每一种情况的分配方法数目，由分类计数原理计算可得答案．

    解答 解：根据题意，分3种情况讨论：
    ①、A，B在一组，C，D，E，F都分在另一组，将两组全排列，对应两个校区即可，有A22=2种分配方法；
    ②、C，D，E，F中取出1人，与A、B一组，剩下3人一组，再将两组全排列，对应两个校区，
    有C41×A22=8种分配方法；
    ③、C，D，E，F中取出2人，与A、B一组，剩下2人一组，再将两组全排列，对应两个校区，
    有C42×A22=12种分配方法；
    故一共有2+8+12=22种分配方法；
    故选：C．

    点评 本题考查排列、组合的应用，关键是依据题意，对其他4人分组，进行分类讨论．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    1．已知f（x）=loga（x-1）+1（a＞0且a≠1）恒过定点M，且点M在直线$\frac{x}{m}+\frac{y}{n}=1$（m＞0，n＞0）上，则m+n的最小值为（　　）
    A．$3+2\sqrt{2}$B．8C．$4\sqrt{2}$D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．在△ABC中，角A、B、C所对的边为a、b、c，且满足cos2A-cos2B=2cos（A-$\frac{π}{6}$）cos（A+$\frac{π}{6}$）．
    （Ⅰ）求角B的值；
    （Ⅱ）若b=$\sqrt{3}$≤a，求2a-c的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

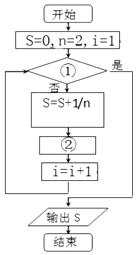
    7．如图给出了计算S=$\frac{1}{2}$+$\frac{1}{4}$+…+$\frac{1}{60}$的值的程序框图，其中 ①②分别是（　　）
    A．i＜30，n=n+2B．i＞30，n=n+2C．i＜30，n=n+1D．i＞30，n=n+1

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．已知函数f（x）=x2，则$\lim_{△x→0}\frac{{f（{△x}）-f（0）}}{△x}$=0．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．在数列{an}中，a1=1，an+1-an=4，则a20的值为77．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．已知函数f（x）=sin2x+2$\sqrt{3}sinxcosx+3{cos^2}$x-2，x∈R，求：
    （1）函数f（x）的最小正周期和单调增区间；
    （2）函数f（x）在区间$[-\frac{π}{6}，\frac{π}{3}]$上的值域．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．已知函数f（x）=ln x，g（x）=$\frac{1}{2}$ax+b．
    （1）若曲线f（x）与曲线g（x）在它们的公共点P（1，f（1））处具有公共切线，求g（x）的表达式；
    （2）若φ（x）=$\frac{m（x-1）}{x+1}$-f（x）在[1，+∞）上是减函数，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．某班某学习小组共7名同学站在一排照相，要求同学甲和乙必须相邻，同学丙和丁不能相邻，则不同的站法共有（　　）种．
    A．$A_5^5A_6^2$B．$A_2^2A_4^4A_4^2$C．$A_2^2A_5^5A_6^2$D．$A_2^2A_4^4A_5^2$

    查看答案和解析>>

    同步练习册答案