
分析 (1)求出函数f(x)的导数,得到关于a的方程,求出a的值,计算g(1)=0,求出b的值,从而求出g(x)的解析式即可;
(2)求出函数的导数,问题转化为2m-2≤x+$\frac{1}{x}$,x∈[1,+∞),根据函数的单调性求出m的范围即可.
解答 解:(1)由已知得f′(x)=$\frac{1}{x}$,所以f′(1)=1=$\frac{1}{2}$a,a=2.
又因为g(1)=0=$\frac{1}{2}$a+b,所以b=-1,所以g(x)=x-1.
(2)因为φ(x)=$\frac{m(x-1)}{x+1}$-f(x)=$\frac{m(x-1)}{x+1}$-ln x在[1,+∞)上是减函数.
所以φ′(x)$\frac{-{x}^{2}+(2m-2)(x-1)}{x(x+1)^{2}}$≤0在[1,+∞)上恒成立.
即x2-(2m-2)x+1≥0在[1,+∞)上恒成立,
则2m-2≤x+$\frac{1}{x}$,x∈[1,+∞),
因为x+$\frac{1}{x}$∈[2,+∞),所以2m-2≤2,m≤2,
故数m的取值范围是(-∞,2].
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及切线方程问题,考查函数恒成立问题,是一道中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $-\frac{{\sqrt{2}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 18种 | B. | 20种 | C. | 22种 | D. | 24种 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
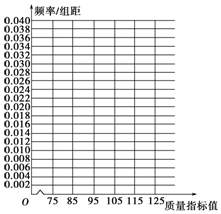 从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量结果得如下频数分布表:
从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量结果得如下频数分布表:| 质量指标值分组 | [75,85) | [85,95) | [95,105) | [105,115) | [115,125) |
| 频数 | 6 | 26 | 38 | 22 | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ① | B. | ② | C. | ①② | D. | ③ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{{\sqrt{2}}}{3}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{5}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 焦虑 | 说谎 | 懒惰 | 总计 | |
| 女生 | 5 | 10 | 15 | 30 |
| 男生 | 20 | 10 | 50 | 80 |
| 总计 | 25 | 20 | 651 | 110 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com