
| 焦虑 | 说谎 | 懒惰 | 总计 | |
| 女生 | 5 | 10 | 15 | 30 |
| 男生 | 20 | 10 | 50 | 80 |
| 总计 | 25 | 20 | 651 | 110 |
分析 对三种心理障碍焦虑、说谎、懒惰分别构造三个随机变量$K_1^2,K_2^2,K_3^2$,
由题中数据分别计算$K_1^2$、$K_2^2$、$K_3^2$的观测值,比较即可得出结论.
解答 解:对三种心理障碍焦虑、说谎、懒惰分别构造三个随机变量$K_1^2,K_2^2,K_3^2$,
由题中数据可得:$K_1^2$的观测值为k1=$\frac{110{×(5×60-25×20)}^{2}}{30×80×20×90}$≈0.8627<2.076,
$K_2^2$的观测值为${k_2}=\frac{{110×{{({10×70-20×10})}^2}}}{30×80×20×90}≈6.366>5.024$,
$K_3^2$的观测值为${k_3}=\frac{{110×{{({15×30-15×50})}^2}}}{30×80×20×90}≈1.410<2.076$;
所以样本数据没有充分的证据显示焦虑与性别有关,
有97.5%的把握认为说谎与性别有关,样本数据没有充分的证据显示懒惰与性别有关.
点评 本题考查了列联表与独立性检验的应用问题,是基础题.


 黄冈创优卷系列答案
黄冈创优卷系列答案科目:高中数学 来源: 题型:选择题
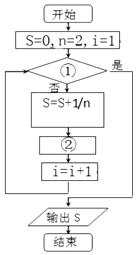
| A. | i<30,n=n+2 | B. | i>30,n=n+2 | C. | i<30,n=n+1 | D. | i>30,n=n+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧(¬q) | B. | (¬p)∧q | C. | p∧q | D. | (¬p)∧(¬q) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{10}$ | B. | $\sqrt{10}$ | C. | $\sqrt{5}$ | D. | -$\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $A_5^5A_6^2$ | B. | $A_2^2A_4^4A_4^2$ | C. | $A_2^2A_5^5A_6^2$ | D. | $A_2^2A_4^4A_5^2$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{6}{7}$ | B. | $\frac{5}{7}$ | C. | $\frac{3}{7}$ | D. | $\frac{1}{7}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com