
分析 根据二项展开式定理的内容,先写出二项式的通项,使得变量x的指数等于8,解出r的值,把r的值代入通项得到这一项的系数.
解答 解:设出所求的项是第r+1项,
则Tr+1=C5rx3(5-r)($\frac{1}{2\sqrt{x}}$)r=($\frac{1}{2}$)rC5rx${\;}^{15-\frac{7}{2}r}$
要求x8的系数,只要使得15-$\frac{7}{2}$r=8,
得r=2,故在求二项式展开式里含x8项的系数为($\frac{1}{2}$)2C52=$\frac{1}{4}×10$=$\frac{5}{2}$.
故答案为:$\frac{5}{2}$
点评 本题考查二项式定理的应用,本题解题的关键是正确写出二项展开式的通项,在这种题目中通项是解决二项展开式的特定项问题的工具.


 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案科目:高中数学 来源: 题型:解答题
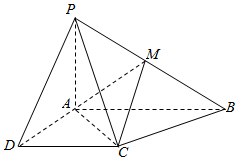 已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,PA=AD=DC=$\frac{1}{2}$AB=1,PM=$\frac{1}{2}$MB.
已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,PA=AD=DC=$\frac{1}{2}$AB=1,PM=$\frac{1}{2}$MB.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,+∞) | B. | (-∞,2) | C. | (2,+∞) | D. | (-∞,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 0 | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com