Question

1．已知圆O以AB为直径，半径为1．若圆O上有长度为1的动弦CD，则$\overrightarrow{AC}•\overrightarrow{BD}$的取值范围是[-$\frac{3}{2}$，$\frac{1}{2}$]．

Answer 1

分析 建立直角坐标系，设出∠BOC=x，用x表示C，D的坐标，求出$\overrightarrow{AC}•\overrightarrow{BD}$的三角表达式，然后化简，即可求解它的范围．

解答 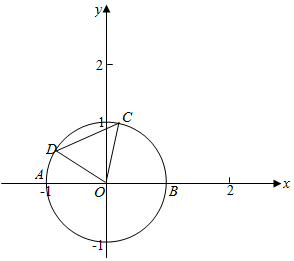解：如图建立平面直角坐标系：设∠BOC=x，则C（cosx，sinx），
∠BOD=x+60°，
D（cos（x+60°），sin（x+60°）），A（-1，0），B（1，0），
则$\overrightarrow{AC}$=（cosx+1，sinx），
$\overrightarrow{BD}$=（cos（x+60°）-1，sin（x+60°）），
则$\overrightarrow{AC}•\overrightarrow{BD}$=（cosx+1）[cos（x+60°）-1]
+sinxsin（x+60°）
=cosxcos（x+60°）-cosx+cos（x+60°）
-1+sinxsin（x+60°）
=cos60°-cosx+cos（x+60°）-1
=-cos（x-60°）-$\frac{1}{2}$，
所以$\overrightarrow{AC}•\overrightarrow{BD}$的取值范围是[-$\frac{3}{2}$，$\frac{1}{2}$]；
故答案为：[-$\frac{3}{2}$，$\frac{1}{2}$]．

点评 本题考查了平面向量的数量积运算；解答本题的关键是正确建立坐标系，利用三角函数表达式求最值．