
 如图,圆O内有一个内接三角形ABC,且直径AB=2,∠ABC=45°,在圆O内随机撒一粒黄豆,则它落在三角形ABC内(阴影部分)的概率是( )
如图,圆O内有一个内接三角形ABC,且直径AB=2,∠ABC=45°,在圆O内随机撒一粒黄豆,则它落在三角形ABC内(阴影部分)的概率是( )| A. | $\frac{1}{2π}$ | B. | $\frac{\sqrt{2}}{2π}$ | C. | $\frac{\sqrt{3}}{2π}$ | D. | $\frac{1}{π}$ |
科目:高中数学 来源: 题型:选择题
| A. | 向左平移$\frac{π}{4}$个单位长度,再把所得各点的横坐标缩短到原来的$\frac{1}{3}$倍 (纵坐标不变) | |
| B. | 向右平移$\frac{π}{4}$个单位长度,再把所得各点的横坐标缩短到原来的$\frac{1}{3}$倍(纵坐标不变) | |
| C. | 向左平移$\frac{π}{4}$个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变) | |
| D. | 向右平移$\frac{π}{4}$个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -4 | B. | 2 | C. | $\frac{8}{3}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 35种 | B. | 70种 | C. | 210种 | D. | 105种 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | -$\frac{4}{5}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,甲、乙两名篮球运动员的季后赛10场得分可用茎叶图表示如图:
如图,甲、乙两名篮球运动员的季后赛10场得分可用茎叶图表示如图:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
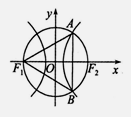 F1、F2分别是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右焦点,以坐标原点O为圆心,|OF2|为半径的圆与该双曲线右支交于A、B两点,若△F1AB是等边三角形,则双曲线的离心率为( )
F1、F2分别是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右焦点,以坐标原点O为圆心,|OF2|为半径的圆与该双曲线右支交于A、B两点,若△F1AB是等边三角形,则双曲线的离心率为( )| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{3}$-1 | D. | 1+$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 22016-1 | B. | 3•21008-3 | C. | 22009-3 | D. | 22010-3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com