Question

3．在锐二面角α-AB-β的面α内一点P到β的距离为P到棱AB的距离的一半，求此二面角的大小．

Answer 1

分析 根据条件作出二面角的平面角，结合直角三角形中的边角关系进行求解即可．

解答 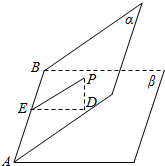解：如图，∵二面角α-AB-β的平面角是锐角θ，
过P作PD⊥β，
平面α内有一点C到β的距离为3，
点C到棱AB距离为4，
作PE⊥AB，连接ED，
则PD⊥AB，
则AB⊥面PED，
则DE⊥AB，
则∠PED=θ，
∵P到β的距离为P到棱AB的距离的一半，
∴PE=2PD，
在直角三角形PDE中，sinθ=$\frac{PD}{PE}=\frac{PE}{2PE}=\frac{1}{2}$，
则θ=30°，
即二面角α-AB-β的大小为30°．

点评 本题主要考查了空间二面角的求解，根据定义作出二面角的平面角是解决本题的关键．