
 �����ڼ䣬���ٹ�·�³�����������ij���鹫˾Ϊ���˽�٣��ڸ������շ�վ��7������С�������а����շ�վ���Ⱥ�˳��ÿ���50���ͳ�ȡһ���ij���������ȡ40���������г������飬��������ij�θ��ٹ�·�ij��٣�km/h�����ֳ�����[60��65����[65��70����[70��75����[75��80����[80��85����[85��90]�õ���ͼ��Ƶ�ʷֲ�ֱ��ͼ��
�����ڼ䣬���ٹ�·�³�����������ij���鹫˾Ϊ���˽�٣��ڸ������շ�վ��7������С�������а����շ�վ���Ⱥ�˳��ÿ���50���ͳ�ȡһ���ij���������ȡ40���������г������飬��������ij�θ��ٹ�·�ij��٣�km/h�����ֳ�����[60��65����[65��70����[70��75����[75��80����[80��85����[85��90]�õ���ͼ��Ƶ�ʷֲ�ֱ��ͼ������ ��1��ѡ��ֱ��ͼ����ߵľ��������ױߵ��е㼴Ϊ�������������߿�ʼС���ε������Ϊ0.5��Ӧ�ĺ�������Ϊ��λ�������ø���С���ε�������Զ�Ӧ���εĵױߵ��е�ĺ�Ϊ���ݵ�ƽ������
��2����ͼ�п�֪��������[60��65���ij������ͳ�����[65��70���ij��������ӳ����ڣ�60��70���ij������γ�ȡ2�����賵����[60��65���ij�����Ϊa��b��������[65��70���ij�����ΪA��B��C��D���г����ԵĻ����¼������Ӷ������Ӧ�ĸ��ʼ��ɣ�
��� �⣺��1�������Ĺ���ֵΪ��ߵľ��ε��е㣬�������Ĺ���ֵΪ77.5����2�֣�
����ͼ��֪����λ��Ӧ����75��80֮�䣬��Ϊm��
��0.01��5+0.02��5+0.04��5+0.06����m-75��=0.5����ã�m=77.5
����λ���Ĺ���ֵΪ77.5����6�֣�
��2����40�����У�������[60��70���Ĺ���5����0.01+0.02����40=6��������
���г�����[65��70������5��0.02��40=4����������ΪA��B��C��D
������[60��65������5��0.01��40=2����������Ϊa��b����8�֣�
�ӳ�����[60��70������6�������������ȡ2���Ŀ��ܽ����15�ֲ�ͬ�Ľ����
���г����2�������ٶ���[65��70���Ľ����6�֡���10�֣�
��Ϊ�鵽ÿ�ֽ�����ǵȿ��ܵģ����Դ���40��������[60��70���������������ȡ2����
�����2�������ٶ���[65��70���ĸ���Ϊ$P=\frac{6}{15}=\frac{2}{5}$����12�֣�
���� ���Ƶ�ʷֲ�ֱ��ͼ���й����������⣬������������߾��εĵױ��е㣻��λ�����������ߵľ��ε������ȵĵױߵ�ֵ��ƽ�������ڸ���С���ε�������Զ�Ӧ�ľ��εĵױ��е�ĺͣ������ͳ�ƺ��ʽ����һ�𣬱Ƚ���ӱ��Ҳ�Ǹ߿��ķ���Ӧ�������ӣ�


 �¿α�ͬ��ѵ��ϵ�д�
�¿α�ͬ��ѵ��ϵ�д� һ����ʦ����Ӧ����������һ��ȫϵ�д�
һ����ʦ����Ӧ����������һ��ȫϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
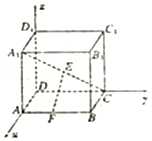 ��ͼ��ʾ���ڿռ�ֱ������ϵ�У�D������ԭ�㣬��һ�ⳤΪa��������ABCD-A1B1C1D1��E��F�ֱ�����Խ���A1C����AB�ϵĶ��㣬��|EF|����СֵΪ��������
��ͼ��ʾ���ڿռ�ֱ������ϵ�У�D������ԭ�㣬��һ�ⳤΪa��������ABCD-A1B1C1D1��E��F�ֱ�����Խ���A1C����AB�ϵĶ��㣬��|EF|����СֵΪ��������| A�� | $\sqrt{2}a$ | B�� | $\frac{{\sqrt{2}}}{2}a$ | C�� | a | D�� | $\frac{1}{2}a$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | 3 | C�� | $\sqrt{3}$ | D�� | $\sqrt{7}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x-2y+6=0 | B�� | x-2y-6=0 | C�� | x+2y-10=0 | D�� | x+2y-8=0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com