
分析 (1)求出导函数$f'(x)=\frac{1}{x-1}-k$,通过当k≤0时,当k>0时,判断导函数的符号,推出函数的单调区间即可.
(2)$g(x)=\frac{1}{3}{x^3}-kx-k+1x∈[{0,1}]$,通过对任意的x1,x2∈[0,1],都有|g(x1)-g(x2)|≤1恒成立,转化为:当x∈[0,1],有gmax(x)-gmin(x)≤1成立,求出g'(x)=x2-k,通过当k≤0时,当k>0时,求解函数的最值,通过gmax(x)-gmin(x)=$g(1)-g(\sqrt{k})=\frac{1}{3}-k+\frac{2}{3}{k^{\frac{3}{2}}}$,令$h(k)=\frac{1}{3}-k+\frac{2}{3}{k^{\frac{3}{2}}}$,$k∈({0,\frac{1}{3}})$,
则$h'(k)={k^{\frac{1}{2}}}-1<0$,利用h(k)在$({0,\frac{1}{3}})$为减函数,求解即可.
解答 解:(1)∵ln(x-1)-k(x-1)+1(x>1),∴$f'(x)=\frac{1}{x-1}-k$,
当k≤0时,f′(x)>0恒成立,故函数在(1,+∞)为增函数,
当k>0时,令f'(x)=0,得$x=\frac{k+1}{k}>1$
当f'(x)<0,即$1<x<\frac{k+1}{k}$时,函数为减函数,
当f'(x)>0,即$x>\frac{k+1}{k}$时,函数为增函数,
综上所述,当k≤0时,函数f(x)在(1,+∞)为增函数,
当k>0时,函数f(x)在$(1,\frac{k+1}{k})$为减函数,在$(\frac{k+1}{k},+∞)$为增函数.
(2)$g(x)=\frac{1}{3}{x^3}-kx-k+1x∈[{0,1}]$,
因为对任意的x1,x2∈[0,1],都有|g(x1)-g(x2)|≤1恒成立
所以当x∈[0,1],有gmax(x)-gmin(x)≤1成立g'(x)=x2-k
当k≤0时,g'(x)=x2-k≥0恒成立,g(x)在[0,1]为增函数
由gmax(x)-gmin(x)=$g(1)-g(0)=\frac{1}{3}-k≤1$得$k≥-\frac{2}{3}$,所以$-\frac{2}{3}≤k≤0$
当k>0时,由g'(x)=x2-k=0得$x=\sqrt{k}$
易知g(x)在$[{0,\sqrt{k}}]$为减函数,在$[{\sqrt{k},+∞})$为增函数
若k≥1,则g(x)在[0,1]为减函数,由gmax(x)-gmin(x)=$g(0)-g(1)=k-\frac{1}{3}≤1$
得$k≤\frac{4}{3}$,所以$1≤k≤\frac{4}{3}$
若$\frac{1}{3}≤k<1$,则g(x)在$[{0,\sqrt{k}}]$为减函数,在$[{\sqrt{k},1}]$为增函数,$g(1)-g(0)=\frac{1}{3}-k≤0$
所以gmax(x)-gmin(x)=$g(0)-g(\sqrt{k})=-\frac{2}{3}{k^{\frac{3}{2}}}$,
而$\frac{1}{3}≤k<1$时$-\frac{2}{3}{k^{\frac{3}{2}}}≤1$恒成立,所以$\frac{1}{3}≤k<1$适合题意
若$0<k<\frac{1}{3}$,则g(x)在$[{0,\sqrt{k}}]$为减函数,在$[{\sqrt{k},1}]$为增函数,$g(1)-g(0)=\frac{1}{3}-k>0$
所以gmax(x)-gmin(x)=$g(1)-g(\sqrt{k})=\frac{1}{3}-k+\frac{2}{3}{k^{\frac{3}{2}}}$,
令$h(k)=\frac{1}{3}-k+\frac{2}{3}{k^{\frac{3}{2}}}$,$k∈({0,\frac{1}{3}})$,
则$h'(k)={k^{\frac{1}{2}}}-1<0$,所以h(k)在$({0,\frac{1}{3}})$为减函数,所以$h(k)<h(0)=\frac{1}{3}<1$,所以$0<k<\frac{1}{3}$适合题意
综上所述:$-\frac{2}{3}≤k≤\frac{4}{3}$.
点评 本题考查函数的导数的应用幂函数的极值以及函数的单调性的应用,考查计算能力与转化思想的应用.


科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
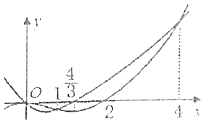 已知函数f(x)与f'(x)的图象如图所示,则函数$g(x)=\frac{f(x)}{e^x}$的单调递增区间为( )
已知函数f(x)与f'(x)的图象如图所示,则函数$g(x)=\frac{f(x)}{e^x}$的单调递增区间为( )| A. | (0,4) | B. | $({-∞,1}),({\frac{4}{3},4})$ | C. | (0,1),(4,+∞) | D. | (-∞,0),(1,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
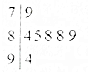 某校高一年级举办歌咏比赛,7位裁判为某班级打出的分数如图茎叶图所示,左边数字表示十位数字,右边数字表示个位数字,则这些数据的中位数是( )
某校高一年级举办歌咏比赛,7位裁判为某班级打出的分数如图茎叶图所示,左边数字表示十位数字,右边数字表示个位数字,则这些数据的中位数是( )| A. | 84 | B. | 85 | C. | 88 | D. | 89 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
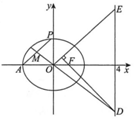 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为为$\frac{1}{2}$,F为椭圆C的右焦点A(-a,0),|AF|=3.
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为为$\frac{1}{2}$,F为椭圆C的右焦点A(-a,0),|AF|=3.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 楹联社 | B. | 书法社 | ||
| C. | 汉服社 | D. | 条件不足无法判断 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com