Question

7．定义在（-1，0）∪（0，1）的偶函数f（x），满足f（$\frac{1}{2}$）=0．当x＞0时，总有（$\frac{1}{x}$-x）f′（x）•ln（1-x²）＞2f（x），则f（x）＜0解集为$\{x丨-1＜x＜-\frac{1}{2}或\frac{1}{2}＜x＜1\}$．

Answer 1

分析 根据偶函数的对称性，利用导函数的性质求函数的单调性，

解答 解：当x＞0时，总有（$\frac{1}{x}$-x）f′（x）•ln（1-x²）＞2f（x）
f′（x）•ln（1-x2）＞$\frac{2x}{1-{x}^{2}}f（x）$，
也就是$f′（x）•ln（1-{x}^{2}）+\frac{-2x}{1-{x}^{2}}f（x）＞0$恒成立，
[ln（1-x²）]′
=[ln（1-x）+ln（1+x）]′
=$\frac{-1}{1-x}+\frac{1}{1+x}$
=$\frac{-2x}{1-{x}^{2}}$
∴[f（x）•ln（1-x²）]′＞0恒成立，
设g（x）=f（x）•ln（1-x²），
则g（x）在（0，1）上单调递增
y=ln（1-x²）是偶函数，函数g（x）=f（x）•ln（1-x²）是偶函数，
∴在（-1，0）上单调递减．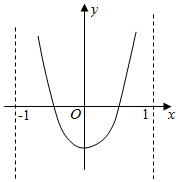
$f（\frac{1}{2}）=f（-\frac{1}{2}）=0$，$g（\frac{1}{2}）=g（-\frac{1}{2}）=g（0）=0$
所以g（x）的图象如下：
$x∈（\frac{1}{2}，1）$，g（x）＞0，而ln（1-x²）＜0，所以f（x）＜0；
$x∈（0，\frac{1}{2}）$，g（x）＜0，而ln（1-x²）＜0，所以f（x）＞0，
函数f（x）的图象对称性可求得解集；
故答案为：$\{x丨-1＜x＜-\frac{1}{2}或\frac{1}{2}＜x＜1\}$

点评 本题考查利用函数的对称性及导函数的性质求函数单调区间，属于中档题．