
分析 (Ⅰ)求导f′(x)=3x2ax+x3axlna=ax(3x2+x3lna),故φ(x)=3x2+x3lna,求导φ′(x)=6x+(3lna)x2,从而可得当x∈(0,2)时,φ′(x)≥0恒成立,从而化为求函数的最值问题即可;
(Ⅱ)当$a=\frac{1}{e}$时,$f(x)=\frac{x^3}{e^x}$,从而化简可得${e^{{x_2}-{x_1}}}<\frac{x_2^3}{x_1^3}$,即3lnx1-3ln(6-x1)+6-2x1<0;令g(x)=3lnx-3ln(6-x)+6-2x,x∈(0,3),从而求导判断函数的单调性即可.
解答 解:(Ⅰ)∵f′(x)=3x2ax+x3axlna=ax(3x2+x3lna),
∴φ(x)=$\frac{f'(x)}{a^x}$=3x2+x3lna,
∴φ′(x)=6x+(3lna)x2,
∵φ(x)=$\frac{f'(x)}{a^x}$是区间(0,2)上的增函数,
∴当x∈(0,2)时,φ′(x)=6x+(3lna)x2≥0恒成立,
即$lna≥-\frac{2}{x}$恒成立;
又x∈(0,2)时,$-\frac{2}{x}∈(-∞,-1)$,
故lna≥-1,
故a≥$\frac{1}{e}$;
即a的最小值为$\frac{1}{e}$.
(Ⅱ)证明:当$a=\frac{1}{e}$时,$f(x)=\frac{x^3}{e^x}$,
∵0<x1<x2且x1+x2=6,
∴0<x1<3,x2=6-x1,
要证f(x1)<f(x2),
只需证$\frac{{{x_1}^3}}{{{e^{x_1}}}}<\frac{{{x_2}^3}}{{{e^{x_2}}}}$(0<x1<3),
只需证${e^{{x_2}-{x_1}}}<\frac{x_2^3}{x_1^3}$,
只需证x2-x1<3lnx2-3lnx1,
只需证3lnx1-3lnx2+x2-x1<0,
只需证3lnx1-3ln(6-x1)+6-2x1<0(*);
设g(x)=3lnx-3ln(6-x)+6-2x,x∈(0,3),
则$g'(x)=\frac{3}{x}+\frac{3}{6-x}-2=\frac{{2{{(x-3)}^2}}}{x(6-x)}$,
当x∈(0,3)时,g′(x)>0,即g(x)在(0,3)上单调递增,
于是对于任意的0<x1<3,g(x1)<g(3)=0,即(*)式成立,
故原命题成立.
点评 本题考查了函数与不等式的关系应用及导数的综合应用,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
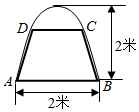 如图,有一块抛物线形钢板,其下口宽为2米,高为2米.计划将此钢板切割成等腰梯形的形状,下底AB是抛物线的下口,上底CD的端点在抛物线上.
如图,有一块抛物线形钢板,其下口宽为2米,高为2米.计划将此钢板切割成等腰梯形的形状,下底AB是抛物线的下口,上底CD的端点在抛物线上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
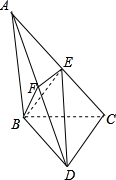 如图所示,在三棱锥A-BCD中,AB⊥平面BCD,BC⊥DC,点E是AC的中点,点F是线段AD上的动点,AB=BC=2.
如图所示,在三棱锥A-BCD中,AB⊥平面BCD,BC⊥DC,点E是AC的中点,点F是线段AD上的动点,AB=BC=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,5) | B. | -4 | C. | -4或20 | D. | -11 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 设全集U={1,2,3,4,5,6},集合A={1,2,4},B={1,3,5},则下列Venn图中阴影部分表示的集合是( )
设全集U={1,2,3,4,5,6},集合A={1,2,4},B={1,3,5},则下列Venn图中阴影部分表示的集合是( )| A. | {1} | B. | {2,4} | C. | {3,5} | D. | {2,3,4,5} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com