【题目】已知B ， C是两个定点，|BC|＝8，且△ABC的周长等于18，求这个三角形的顶点A的轨迹方程．
【答案】【解答】
以过B、C两点的直线为x轴，线段BC的垂直平分线为y轴，建立平面直角坐标系xOy.
如图所示．由|BC|＝8，可知点B(－4,0)，C(4,0)，c＝4.
由|AB|＋|AC|＋|BC|＝18，|BC|＝8，得|AB|＋|AC|＝10，
因此，点A的轨迹是以B、C为焦点的椭圆，这个椭圆上的点与两焦点的距离之和2a＝10，但点A不在x轴上．由a＝5，c＝4，得b2＝a2－c2＝25－16＝9.所以点A的轨迹方程为 
(y≠0)．
【解析】利用椭圆的定义求动点的轨迹方程，应先根据动点具有的条件，验证是否符合椭圆的定义，即动点到两定点距离之和是否是一常数，且该常数(定值)大于两点的距离，若符合，则动点的轨迹为椭圆，然后确定椭圆的方程，这就是定义法求椭圆标准方程的方法，但注意检验．
阅读快车系列答案科目：高中数学 来源： 题型：
【题目】已知 
,函数 f(x)=x2(x-a) ,若f'(1)=1 .
（1）求 a 的值并求曲线 y=f(x) 在点(1,f(1)) 处的切线方程y=g(x) ；
（2）设h(x)=f'(x)+g(x) ,求 h(x) 在 [0,1] 上的最大值与最小值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，两个椭圆
， 
内部重叠区域的边界记为曲线C，P是曲线C上的任意一点，给出下列四个判断：
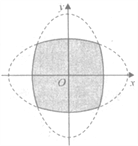
①P到F1（－4，0）、F2（4，0）、E1（0，－4）、E2（0，4）四点的距离之和为定值；
②曲线C关于直线y＝x、y＝－x均对称；③曲线C所围区域面积必小于36．
④曲线C总长度不大于6π．上述判断中正确命题的序号为________________．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）= 
为偶函数，方程f（x）=m有四个不同的实数解，则实数m的取值范围是（ ）
A.（﹣3，﹣1）
B.（﹣2，﹣1）
C.（﹣1，0）
D.（1，2）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知动点M(x,y)到直线l：x=4的距离是它到点N(1,0)的距离的2倍.
（1）求动点M的轨迹C的方程;
（2）过点P(0,3)的直线m与轨迹C交于A,B两点.若A是PB的中点,求直线m的斜率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知圆C：x2+y2﹣6x﹣4y+4=0，点P（6，0）．
（1）求过点P且与圆C相切的直线方程l；
（2）若圆M与圆C外切，且与x轴切于点P，求圆M的方程．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如今我们的互联网生活日益丰富，除了可以很方便地网购，网上叫外卖也开始成为不少人日常生活中不可或缺的一部分.为了解网络外卖在
市的普及情况，市某调查机构借助网络进行了关于网络外卖的问卷调查，并从参与调查的网民中抽取了200人进行抽样分析，得到下表：（单位：人）
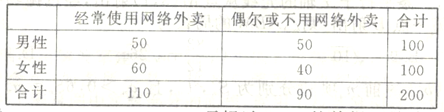
（1）根据以上数据，能否在犯错误的概率不超过0.15的前提下认为市使用网络外卖的情况与性别有关？
（2）①现从所抽取的女网民中利用分层抽样的方法再抽取5人，再从这5人中随机选出3人赠送外卖优惠券，求选出的3人中至少有2人经常使用网络外卖的概率；
②将频率视为概率，从市所有参与调查的网民中随机抽取10人赠送礼品，记其中经常使用网络外卖的人数为
，求的数学期望和方差.
参考公式：
，其中
.
参考数据：
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
