
| 3 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
| 3 |
| ||
| 2 |
| ||
| 2 |
| 3 |
| 3 |


 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:高中数学 来源: 题型:
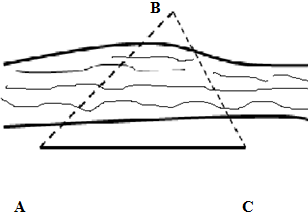 如图,在一次测量活动中,要测量河两岸B、C两点间的距离,测量者在河的一侧,测得AC=24m,∠BAC=45°,∠ACB=75°,求B、C两点间的距离.
如图,在一次测量活动中,要测量河两岸B、C两点间的距离,测量者在河的一侧,测得AC=24m,∠BAC=45°,∠ACB=75°,求B、C两点间的距离.查看答案和解析>>
科目:高中数学 来源: 题型:
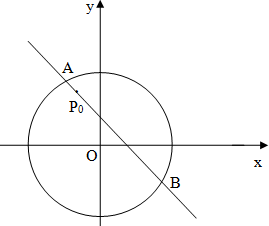 如图,圆x2+y2=8内有一点P0(-1,2),AB为过点P0且倾斜角为α的弦.
如图,圆x2+y2=8内有一点P0(-1,2),AB为过点P0且倾斜角为α的弦.查看答案和解析>>
科目:高中数学 来源: 题型:
| 1+ln(x-1) |
| x-a |
| m |
| x |
| 1 |
| 2 |
| 2 |
| 3 |
| 3 |
| 4 |
| n |
| n+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
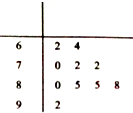 为了保护生态和环境,某市不再完全以GDP考核辖区内各县政府的政绩,广大群众的幸福指数成为考核县政府政绩的又一个重要指标,从而成立了市政府幸福办公室,其主要工作是随机抽查群众的幸福指数,为市政府提供最基础的原始数据.该办公室某工作人员在一次随机抽查了10名A县群众后,绘制了如图的茎叶图.
为了保护生态和环境,某市不再完全以GDP考核辖区内各县政府的政绩,广大群众的幸福指数成为考核县政府政绩的又一个重要指标,从而成立了市政府幸福办公室,其主要工作是随机抽查群众的幸福指数,为市政府提供最基础的原始数据.该办公室某工作人员在一次随机抽查了10名A县群众后,绘制了如图的茎叶图.| 1 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com