
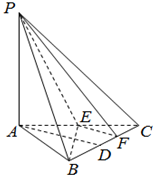
 在三棱锥P-ABC中,PA⊥平面ABC,△ABC为正三角形,D、E分别为BC、CA的中点,F为CD的中点.若在线段PB上存在一点Q,使得平面ADQ∥平面PEF.
在三棱锥P-ABC中,PA⊥平面ABC,△ABC为正三角形,D、E分别为BC、CA的中点,F为CD的中点.若在线段PB上存在一点Q,使得平面ADQ∥平面PEF.分析 (1)由平面ADQ∥平面PEF,结合面面平行的性质得DQ∥PF,AQ∥EF,再由平行线截线段成比例得$\frac{PQ}{QB}$的值;
(2)直接利用等积法求得三棱锥Q-PEF的体积;
(3)连PD、QF交于点O,过O在平面PAD内作AD的平行线OM交PA于点M,则M点为所求点,再由平行线截线段成比例得AM.
解答 解(1)由平面ADQ∥平面PEF,得DQ∥PF,AQ∥EF,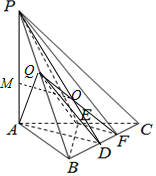
∴$\frac{PQ}{QB}=\frac{DF}{BD}=\frac{1}{2}$;
(2)VQ-PEF=VD-PEF=$\frac{1}{3}{V}_{B-PEF}=\frac{1}{3}{V}_{P-BEF}$=$\frac{1}{3}•(\frac{3}{4}•\frac{1}{2}•2•2\sqrt{3})•4$=$2\sqrt{3}$;
(3)连PD、QF交于点O,过O在平面PAD内作AD的平行线OM交PA于点M,则M点为所求点,
∴$\frac{PM}{AM}=\frac{PO}{OD}=\frac{PF}{QD}=\frac{BF}{BD}=\frac{3}{2}$,
∴$\frac{AM}{AP}=\frac{2}{5}$,则$AM=\frac{2}{5}AP=\frac{8}{5}$.
点评 本题考查平面与平面平行的性质,训练了利用等积法求多面体的体积,考查空间想象能力和思维能力,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | 对于?m∈(1,3),曲线C为一个椭圆 | B. | ?m∈(-∞,1)∪(3,+∞)使曲线C不是双曲线 | ||
| C. | 对于?m∈R,曲线C一定不是直线 | D. | ?m∈(1,3)使曲线C不是椭圆 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{\sqrt{7}}{2}$ | B. | $\frac{\sqrt{7}}{2}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1-a | B. | 2-a | C. | 1+a | D. | 2+a |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 钝角三角形 | B. | 直角三角形 | C. | 等腰直角三角形 | D. | 等边三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com