
| A. | 对于?m∈(1,3),曲线C为一个椭圆 | B. | ?m∈(-∞,1)∪(3,+∞)使曲线C不是双曲线 | ||
| C. | 对于?m∈R,曲线C一定不是直线 | D. | ?m∈(1,3)使曲线C不是椭圆 |
分析 对于所给的方程,当m=1、m=3时,易得方程表示的图形;当m≠1,且 m≠3时,方程即$\frac{{x}^{2}}{m-3}+\frac{{y}^{2}}{m-1}$=1,再分3-m=m-1、(3-m)(m-1)大于零、小于零三种情况,分别求得方程表示的曲线形状,综合可得结论.
解答 解:对于方程(m-1)x2+(3-m)y2=(m-1)(3-m),①当m=1时,方程即2y2=0,即 y=0,表示x轴;
②当m=3时,方程即2x2=0,即 x=0,表示y轴;
③当m≠1,且 m≠3时,方程即$\frac{{x}^{2}}{m-3}+\frac{{y}^{2}}{m-1}$=1,
若3-m=m-1,即m=2时,方程即为圆:x2+y2=1,表示一个单位圆;
若(3-m)(m-1)<0,即m>3或者m<1时,方程表示双曲线;
若(3-m)(m-1)>0且3-m≠m-1,即1<m<3,且m≠2时,方程表示椭圆.
综合可得:当m=1,方程表示x轴,当m=3;方程表示y轴;当m=2时,方程表示圆;当1<m<3且不等于2时,方程表示椭圆;
当m>3或者m<1时,方程表示双曲线.
故选D.
点评 本题主要考查二元二次方程表示圆的条件,体现了分类讨论的数学思想,属于基础题.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\frac{4\sqrt{6}}{5}$ | C. | $\sqrt{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ∅ | B. | {d} | C. | {a,c} | D. | {b,e} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 时间t | $\frac{1}{2}$ | 2 | 4 |
| 高度h | 10 | 25 | 17 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{1}{2}$,2] | B. | (-1,+∞) | C. | (-$\frac{1}{2}$,0)∪(0,2) | D. | (-$\frac{1}{2}$,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
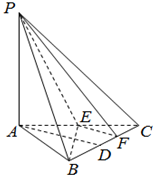 在三棱锥P-ABC中,PA⊥平面ABC,△ABC为正三角形,D、E分别为BC、CA的中点,F为CD的中点.若在线段PB上存在一点Q,使得平面ADQ∥平面PEF.
在三棱锥P-ABC中,PA⊥平面ABC,△ABC为正三角形,D、E分别为BC、CA的中点,F为CD的中点.若在线段PB上存在一点Q,使得平面ADQ∥平面PEF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com