
| A. | $6\sqrt{2}$ | B. | $4\sqrt{3}$ | C. | 5 | D. | $5\sqrt{2}$ |
分析 利用三角形面积计算公式、正弦定理余弦定理即可得出.
解答 解:∵$S=\frac{1}{2}acsinB=\frac{1}{2}×1×c×\frac{{\sqrt{2}}}{2}=\frac{{\sqrt{2}}}{4}c=2$,∴$c=4\sqrt{2}$,
由余弦定理得${b^2}={a^2}+{c^2}-2accosB={1^2}+{({4\sqrt{2}})^2}-2•1•4\sqrt{2}•\frac{{\sqrt{2}}}{2}=33-8=25$,
∴b=5.
由正弦定理$2R=\frac{b}{sinB}=\frac{5}{{\frac{{\sqrt{2}}}{2}}}=5\sqrt{2}$(R为△ABC外接圆半径),
故选:D.
点评 本题考查了三角形面积计算公式、正弦定理余弦定理,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{5π}{6}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,1] | B. | (0,1) | C. | (-∞,0]∪[1,+∞) | D. | (-∞,0)∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ab<ac | B. | ac<bc | C. | a|b|>c|b| | D. | a2>b2>c2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
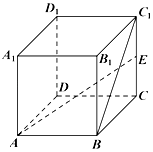 长方体ABCD-A1B1C1D1中AB=AA1=2,AD=1,E为CC1的中点且$AE=\sqrt{6}$,则异面直线BC1与AE所成角的余弦值为( )
长方体ABCD-A1B1C1D1中AB=AA1=2,AD=1,E为CC1的中点且$AE=\sqrt{6}$,则异面直线BC1与AE所成角的余弦值为( )| A. | $\frac{\sqrt{10}}{10}$ | B. | $\frac{\sqrt{30}}{10}$ | C. | $\frac{2\sqrt{15}}{10}$ | D. | $\frac{3\sqrt{10}}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 对于任意向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$,若$\overrightarrow{a}$∥$\overrightarrow{b}$,$\overrightarrow{b}$∥$\overrightarrow{c}$,则$\overrightarrow{a}$∥$\overrightarrow{c}$ | |
| B. | 若向量$\overrightarrow{a}$与$\overrightarrow{b}$同向,且|$\overrightarrow{a}$|>|$\overrightarrow{b}$|,则$\overrightarrow{a}$>$\overrightarrow{b}$. | |
| C. | 向量$\overrightarrow{AB}$与$\overrightarrow{CD}$是共线向量,则A、B、C、D四点一定共线 | |
| D. | 单位向量的模都相等 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com