
【题目】设函数![]() ,其中
,其中![]() .
.
(1)当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)讨论函数![]() 的单调性;
的单调性;
(3)当![]() ,且
,且![]() 时证明不等式:
时证明不等式: ![]()
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源: 题型:
【题目】某小组共10人,利用假期参加义工活动,已知参加义工活动1次的有2人,2次的有4人,3次的有4人.现从这10人中随机选出2人作为该组代表参加座谈会.
(1)设![]() 为事件“选出的2人参加义工活动次数之和为4”,求事件
为事件“选出的2人参加义工活动次数之和为4”,求事件![]() 发生的概率;
发生的概率;
(2)设![]() 为选出的2人参加义工活动次数之差的绝对值,求随机变量
为选出的2人参加义工活动次数之差的绝对值,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
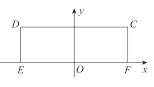
【题目】已知长方形![]() ,
, ![]() ,
, ![]() ,以
,以![]() 的中点
的中点![]() 为原点,建立如图所示的平面直角坐标系
为原点,建立如图所示的平面直角坐标系![]() .
.
(1)求以![]() 为焦点,且过
为焦点,且过![]() 两点的椭圆的标准方程;
两点的椭圆的标准方程;
(2)在(1)的条件下,过点![]() 作直线
作直线![]() 与椭圆交于不同的两点
与椭圆交于不同的两点![]() ,设
,设![]() ,点
,点![]() 坐标为
坐标为![]() ,若
,若![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂需要确定加工某大型零件所花费的时间,连续4天做了4次统计,得到的数据如下:
零件的个数 | 2 | 3 | 4 | 5 |
加工的时间 | 2.5 | 3 | 4 | 5.5 |
(1)在直角坐标系中画出以上数据的散点图,求出![]() 关于
关于![]() 的回归方程
的回归方程![]() ,并在坐标系中画出回归直线;
,并在坐标系中画出回归直线;
(2)试预测加工10个零件需要多少时间?
参考公式:两个具有线性关系的变量的一组数据:![]() ,
,
其回归方程为![]() ,其中
,其中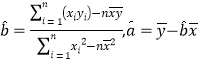
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地高中年级学生某次身体素质体能测试的原始成绩采用百分制,已知这些学生的原始成绩均分布在![]() 内,发布成绩使用等级制,各等级划分标准见下表,并规定:
内,发布成绩使用等级制,各等级划分标准见下表,并规定: ![]() 三级为合格,
三级为合格, ![]() 级为不合格
级为不合格
 为了了解该地高中年级学生身体素质情况,从中抽取了
为了了解该地高中年级学生身体素质情况,从中抽取了![]() 名学生的原始成绩作为样本进行统计,按照
名学生的原始成绩作为样本进行统计,按照![]() 分组作出频率分布直方图如图
分组作出频率分布直方图如图![]() 所示,样本中分数在
所示,样本中分数在![]() 分及以上的所有数据的茎叶图如图
分及以上的所有数据的茎叶图如图![]() 所示.
所示.
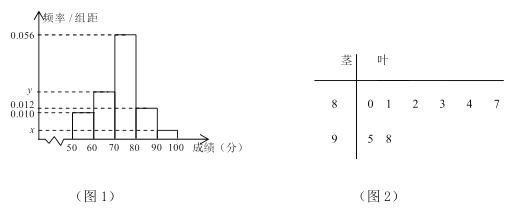
(Ⅰ) 求![]() 及频率分布直方图中
及频率分布直方图中![]() 的值;
的值;
(Ⅱ) 根据统计思想方法,以事件发生的频率作为相应事件发生的概率,若在该地高中学生中任选![]() 人,求至少有
人,求至少有![]() 人成绩是合格等级的概率;
人成绩是合格等级的概率;
(Ⅲ)上述容量为![]() 的样本中,从
的样本中,从![]() 两个等级的学生中随机抽取了
两个等级的学生中随机抽取了![]() 名学生进行调研,记
名学生进行调研,记![]() 为所抽取的
为所抽取的![]() 名学生中成绩为
名学生中成绩为![]() 等级的人数,求随机变量
等级的人数,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(A)在直角坐标系![]() 中,以坐标原点为极点,
中,以坐标原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的参数方程为
的参数方程为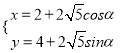 (
(![]() 为参数),
为参数), ![]() 是曲线
是曲线![]() 上的动点,
上的动点, ![]() 为线段
为线段![]() 的中点,设点
的中点,设点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求![]() 的坐标方程;
的坐标方程;
(2)若射线![]() 与曲线
与曲线![]() 异于极点的交点为
异于极点的交点为![]() ,与曲线
,与曲线![]() 异于极点的交点为
异于极点的交点为![]() ,求
,求![]() .
.
(B)设函数![]() .
.
(1)当![]() 时,求不等式
时,求不等式![]() 的解集;
的解集;
(2)对任意![]() ,
, ![]() 不等式
不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂生产![]() 和
和![]() 两种产品,按计划每天生产
两种产品,按计划每天生产![]() 各不得少于10吨,已知生产
各不得少于10吨,已知生产![]() 产品
产品![]() 吨需要用煤9吨,电4度,劳动力3个(按工作日计算).生产
吨需要用煤9吨,电4度,劳动力3个(按工作日计算).生产![]() 产品1吨需要用煤4吨,电5度,劳动力10个,如果
产品1吨需要用煤4吨,电5度,劳动力10个,如果![]() 产品每吨价值7万元,
产品每吨价值7万元, ![]() 产品每吨价值12万元,而且每天用煤不超过300吨,用电不超过200度,劳动力最多只有300个,每天应安排生产
产品每吨价值12万元,而且每天用煤不超过300吨,用电不超过200度,劳动力最多只有300个,每天应安排生产![]() 两种产品各多少才是合理的?
两种产品各多少才是合理的?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com