
分析 (1)由新定义得$\left\{\begin{array}{l}{{3}^{x}•cosy=3}\\{{3}^{x}siny=0}\end{array}\right.$,由此能求出相应的复数z.
(2)分别求出g(2+$\frac{π}{4}i$i)、g(-1+$\frac{π}{4}$i)和g(1+$\frac{π}{2}$i),由此能求出g(2+$\frac{π}{4}$i)•g(-1+$\frac{π}{4}$i)=g(1+$\frac{π}{2}$i).由此发现一个更一般的等式为:g(b+2kπ)=g(b),利用三角函数性质进行证明.
解答 解:(1)∵对任意复数z=x+yi(x、y∈R),定义g(z)=3x(cosy+isiny),g(z)=3,
∴由$\left\{\begin{array}{l}{{3}^{x}•cosy=3}\\{{3}^{x}siny=0}\end{array}\right.$,得$\left\{\begin{array}{l}{cosy=1}\\{{3}^{x}=3}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=1}\\{y=2kπ,k∈Z}\end{array}\right.$,
∴z=1+2kπi,k∈Z.
(2)∵g(2+$\frac{π}{4}i$i)=9($\frac{\sqrt{2}}{2}$+$\frac{\sqrt{2}}{2}$i),
g(-1+$\frac{π}{4}$i)=$\frac{1}{3}$($\frac{\sqrt{2}}{2}$+$\frac{\sqrt{2}}{2}$i),
g(1+$\frac{π}{2}$i)=3i,
∴g(2+$\frac{π}{4}$i)•g(-1+$\frac{π}{4}$i)=g(1+$\frac{π}{2}$i).
由此发现一个更一般的等式为:g(b+2kπ)=g(b).
证明如下:
∵$\left\{\begin{array}{l}{cos(b+2kπ)=cosb}\\{sin(b+2kπ)=sinb}\end{array}\right.$,
∴$\left\{\begin{array}{l}{{3}^{a}cos(b+2kπ)={3}^{a}cosb}\\{{3}^{a}sin(b+2kπ)={3}^{a}sinb}\end{array}\right.$,
∴g(b+2kπ)=g(b).
点评 将复数问题转化为实数问题来研究是解决复数问题的一种重要思想方法,而实现转化的桥梁是复数相等的条件.此外本题涉及到三角函数的运算.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
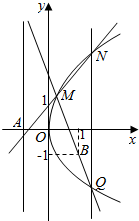 如图所示,已知点A(-1,0)是抛物线的准线与x轴的焦点,过点A的直线与抛物线交于M,N两点,过点M的直线交抛物线于另一个点Q,且直线MQ过点B(1,-1).
如图所示,已知点A(-1,0)是抛物线的准线与x轴的焦点,过点A的直线与抛物线交于M,N两点,过点M的直线交抛物线于另一个点Q,且直线MQ过点B(1,-1).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | -$\frac{3}{4}$ | D. | -$\frac{4}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com