
分析 (1)求出二次函数的对称轴方程,讨论对称轴和区间[-1,1]的关系,求出函数的最值即可;
(2)设m<x1<x2<m+1,m为整数.分类讨论k的存在性,综合讨论结果,可得答案.
解答 解:(1)当b=1时,f(x)=(x+$\frac{a}{2}$)2+1-$\frac{{a}^{2}}{4}$,对称轴为x=-$\frac{a}{2}$,
当a≤-2时,函数f(x)在[-1,1]上递减,则函数的最大值为:f(-1)=-a;最小值为:f(1)=a.
函数f(x)在[-1,1]上的值域:[a,-a].
当0<a≤2时,即有-1≤-$\frac{a}{2}$<0,函数的最小值:f(-$\frac{a}{2}$)=1-$\frac{{a}^{2}}{4}$;最大值为:f(1)=2+a.
函数f(x)在[-1,1]上的值域:[1-$\frac{{a}^{2}}{4}$,2-a].
当-2<a≤0时,0≤-$\frac{a}{2}$<1,函数f(x)的最小值为:f(-$\frac{a}{2}$)=1-$\frac{{a}^{2}}{4}$;最大值为:f(-1)=2-a.
函数f(x)在[-1,1]上的值域:[1-$\frac{{a}^{2}}{4}$,2+a].
当a>2时,$-\frac{a}{2}$<-1,函数f(x)在[-1,1]上递减,
则函数的最小值为:f(-1)=-a;最大值为:f(1)=a.
函数f(x)在[-1,1]上的值域:[-a,a].…(6分)
(2)设m<x1<x2<m+1,m为整数.
则△=a2-4b>0,即b<$\frac{{a}^{2}}{4}$,
①当-$\frac{a}{2}$∈(m,m+$\frac{1}{2}$],即-1≤a+2m<0时,
f(m)=m2+am+b<m2+am+$\frac{{a}^{2}}{4}$=(m+$\frac{a}{2}$)2≤$\frac{1}{4}$;
②当-$\frac{a}{2}$∈(m+$\frac{1}{2}$,m+1),即-2<a+2m<-1时,
f(m+1)=(m+1)2+a(m+1)+b<(m+2)2+a(m+1)+$\frac{{a}^{2}}{4}$=(m+1+$\frac{a}{2}$)2≤$\frac{1}{4}$;
综上,存在整数k,使得|f(k)|≤$\frac{1}{4}$.…(12分)
点评 本题考查的知识点是二次函数的图象和性质,分类讨论思想,熟练掌握二次函数的图象和性质,是解答的关键.


 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | y=3x | B. | y=2x(-1≤x<1) | ||
| C. | $y=\left\{\begin{array}{l}{x^2}+x,x>0\\{x^2}-x,x<0\end{array}\right.$ | D. | y=2x-2-x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 房41017 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| A户型 | 2.6 | 2.7 | 2.8 | 2.8 | 2.9 | 3.2 | 2.9 | 3.1 | 3.4 | 3.3 | 3.4 | 3.3 |
| B户型 | 3.6 | 3.7 | 3.7 | 3.9 | 3.8. | 3.9 | 4.3 | 4.4 | 4.1 | 4.2 | 4.3 | 4.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
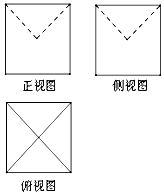 某几何体的三视图如图所示,图中的四边形都是边长为2的正方形,正视图和侧视图中的两条虚线都互相垂直且相等,则该几何体的体积是( )
某几何体的三视图如图所示,图中的四边形都是边长为2的正方形,正视图和侧视图中的两条虚线都互相垂直且相等,则该几何体的体积是( )| A. | $8-\frac{π}{3}$ | B. | $8-\frac{π}{6}$ | C. | $\frac{20}{3}$ | D. | $\frac{16}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,+∞) | B. | (-∞,0) | C. | (0,1] | D. | (-∞,1] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com