Question

【题目】为提高黔东南州的整体旅游服务质量，州旅游局举办了黔东南州旅游知识竞赛，参赛单位为本州内各旅游协会，参赛选手为持证导游.现有来自甲旅游协会的导游3名，其中高级导游2名；乙旅游协会的导游3名，其中高级导游1名.从这6名导游中随机选择2人 参加比赛.

（Ⅰ）求选出的2人都是高级导游的概率；

（Ⅱ）为了进一步了解各旅游协会每年对本地经济收入的贡献情况，经多次统计得到，甲旅游协会对本地经济收入的贡献范围是（单位：万元），乙旅游协会对本地经济收入的贡献范围是（单位：万元），求甲旅游协会对本地经济收入的贡献不低于乙旅游协会对本地经济收入的贡献的概率.

Answer 1

【答案】(1) 选出的人都是高级导游的概率为 ;(2) .

【解析】试题分析：（1）利用穷举法，得；（2）由题意，本题是面积型几何概型，解得.

试题解析：

(Ⅰ)设来自甲旅游协会的名导游为，其中为高级导游，

来自乙旅游协会的名导游为，其中为高级导游，

从这名导游中随机选择人参加比赛，有下列基本情况：;

; ; ;共种，

其中选出的人都是高级导游的有 ，共种

所以选出的人都是高级导游的概率为 .

(Ⅱ)依题意，设甲旅游协会对本地经济收入的贡献为（单位：万元），

乙旅游协会对本地经济收入的贡献为（单位：万元），则且，

若甲旅游协会对本地经济收入的贡献不低于乙旅游协会对本地经济收入的贡献，

则，属于几何概型问题

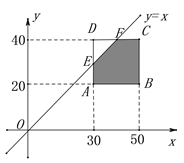
作图，由图可知 ，

所求概率为.