
【题目】二进制规定:每个二进制数由若干个0、1组成,且最高位数字必须为1.若在二进制中,![]() 是所有
是所有![]() 位二进制数构成的集合,对于
位二进制数构成的集合,对于![]() ,
,![]() ,
,![]() 表示
表示![]() 和
和![]() 对应位置上数字不同的位置个数.例如当
对应位置上数字不同的位置个数.例如当![]() ,
,![]() 时
时![]() ,当
,当![]() ,
,![]() 时
时![]() .
.
(1)令![]() ,求所有满足
,求所有满足![]() ,且
,且![]() 的
的![]() 的个数;
的个数;
(2)给定![]() ,对于集合
,对于集合![]() 中的所有
中的所有![]() ,求
,求![]() 的和.
的和.
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案科目:高中数学 来源: 题型:
【题目】依据某地某条河流8月份的水文观测点的历史统计数据所绘制的频率分布直方图如图(甲)所示;依据当地的地质构造,得到水位与灾害等级的频率分布条形图如图(乙)所示.
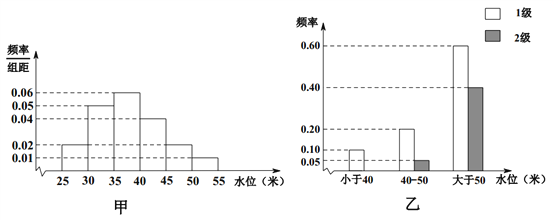
试估计该河流在8月份水位的中位数;
(1)以此频率作为概率,试估计该河流在8月份发生1级灾害的概率;
(2)该河流域某企业,在8月份,若没受1、2级灾害影响,利润为500万元;若受1级灾害影响,则亏损100万元;若受2级灾害影响则亏损1000万元.
现此企业有如下三种应对方案:
方案 | 防控等级 | 费用(单位:万元) |
方案一 | 无措施 | 0 |
方案二 | 防控1级灾害 | 40 |
方案三 | 防控2级灾害 | 100 |
试问,如仅从利润考虑,该企业应选择这三种方案中的哪种方案?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为提高黔东南州的整体旅游服务质量,州旅游局举办了黔东南州旅游知识竞赛,参赛单位为本州内各旅游协会,参赛选手为持证导游.现有来自甲旅游协会的导游3名,其中高级导游2名;乙旅游协会的导游3名,其中高级导游1名.从这6名导游中随机选择2人 参加比赛.
(Ⅰ)求选出的2人都是高级导游的概率;
(Ⅱ)为了进一步了解各旅游协会每年对本地经济收入的贡献情况,经多次统计得到,甲旅游协会对本地经济收入的贡献范围是![]() (单位:万元),乙旅游协会对本地经济收入的贡献范围是
(单位:万元),乙旅游协会对本地经济收入的贡献范围是![]() (单位:万元),求甲旅游协会对本地经济收入的贡献不低于乙旅游协会对本地经济收入的贡献的概率.
(单位:万元),求甲旅游协会对本地经济收入的贡献不低于乙旅游协会对本地经济收入的贡献的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据中国日报网报道:2017年11月13日,TOP500发布的最新一期全球超级计算机500强榜单显示,中国超算在前五名中占据两席,其中超算全球第一“神威太湖之光”完全使用了国产品牌处理器。为了了解国产品牌处理器打开文件的速度,某调查公司对两种国产品牌处理器进行了12次测试,结果如下(数值越小,速度越快,单位是MIPS)
测试1 | 测试2 | 测试3 | 测试4 | 测试5 | 测试6 | 测试7 | 测试8 | 测试9 | 测试10 | 测试11 | 测试12 | |
品牌A | 3 | 6 | 9 | 10 | 4 | 1 | 12 | 17 | 4 | 6 | 6 | 14 |
品牌B | 2 | 8 | 5 | 4 | 2 | 5 | 8 | 15 | 5 | 12 | 10 | 21 |
设![]() 分别表示第次测试中品牌A和品牌B的测试结果,记
分别表示第次测试中品牌A和品牌B的测试结果,记![]()
![]()
(Ⅰ)求数据![]() 的众数;
的众数;
(Ⅱ)从满足![]() 的测试中随机抽取两次,求品牌A的测试结果恰好有一次大于品牌B的测试结果的概率;
的测试中随机抽取两次,求品牌A的测试结果恰好有一次大于品牌B的测试结果的概率;
(Ⅲ)经过了解,前6次测试是打开含有文字和表格的文件,后6次测试是打开含有文字和图片的文件.请你依据表中数据,运用所学的统计知识,对这两种国产品牌处理器打开文件的速度进行评价.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() ,若椭圆
,若椭圆![]() :
:![]() ,则称椭圆
,则称椭圆![]() 与椭圆
与椭圆![]() “相似”.
“相似”.

(1)求经过点![]() ,且与椭圆
,且与椭圆![]() :
:![]() “相似”的椭圆
“相似”的椭圆![]() 的方程;
的方程;
(2)若![]() ,椭圆
,椭圆![]() 的离心率为
的离心率为![]() ,
,![]() 在椭圆
在椭圆![]() 上,过
上,过![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点,且
两点,且![]() .
.
①若![]() 的坐标为
的坐标为![]() ,且
,且![]() ,求直线
,求直线![]() 的方程;
的方程;
②若直线![]() ,
,![]() 的斜率之积为
的斜率之积为![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),在以坐标原点为极点,
),在以坐标原点为极点,![]() 轴非负轴为极轴的极坐标系中,曲线
轴非负轴为极轴的极坐标系中,曲线![]() :
:![]() (
(![]() 为极角).
为极角).
(1)将曲线![]() 化为极坐标方程,当
化为极坐标方程,当![]() 时,将
时,将![]() 化为直角坐标方程;
化为直角坐标方程;
(2)若曲线![]() 与
与![]() 相交于一点
相交于一点![]() ,求
,求![]() 点的直角坐标使
点的直角坐标使![]() 到定点
到定点![]() 的距离最小.
的距离最小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,已知直角梯形ABCD中,![]() ,AB//DC,AB⊥AD,E为CD的中点,沿AE把△DAE折起到△PAE的位置(D折后变为P),使得PB=2,如图2.
,AB//DC,AB⊥AD,E为CD的中点,沿AE把△DAE折起到△PAE的位置(D折后变为P),使得PB=2,如图2.
(Ⅰ)求证:平面PAE⊥平面ABCE;
(Ⅱ)求点B到平面PCE的距离.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抛物线![]() ,
,![]() ,
,![]() 为抛物线的焦点,
为抛物线的焦点,![]() 是抛物线上两点,线段
是抛物线上两点,线段![]() 的中垂线交
的中垂线交![]() 轴于
轴于![]() ,
,![]() ,
,![]() 。
。
(Ⅰ)证明:![]() 是
是![]() 的等差中项;
的等差中项;
(Ⅱ)若![]() ,
,![]() 为平行于
为平行于![]() 轴的直线,其被以AD为直径的圆所截得的弦长为定值,求直线
轴的直线,其被以AD为直径的圆所截得的弦长为定值,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在边长为4的菱形![]() 中,
中,![]() ,点
,点![]() 分别是边
分别是边![]() 的中点,
的中点,![]() ,沿
,沿![]() 将
将![]() 翻折到
翻折到![]() ,连接
,连接![]() ,得到如图所示的五棱锥,且
,得到如图所示的五棱锥,且![]() .
.
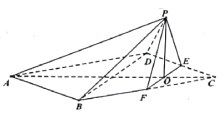
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成二面角的余弦值.
所成二面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com