
分析 (1)求导,求得f(x)在(1,f(1))切线方程,即可求得m的值,由f(x)在(0,1)内是增函数,则f′(x)=$\frac{a}{x}$-$\frac{2}{(x+1)^{2}}$≥0在(0,1)内恒成立,a≥$\frac{2x}{(x+1)^{2}}$在(0,1)内恒成立;
(2)先求出导函数,求出切线方程,构造出新函数,换元,根据寒酸的单调性即可求得的单调性,求得x0>0,根据指数函数的性质,即可求得g(x0)>1.
解答 解:(1)求导f′(x)=$\frac{a}{x}$-$\frac{2}{(x+1)^{2}}$,由f′(1)=a-$\frac{1}{2}$,f(1)=1-m,
则切线方程y-f(1)=f′(1)(x-1),y=(a-$\frac{1}{2}$)x-(a-$\frac{1}{2}$)+1-m,
∴-(a-$\frac{1}{2}$)+1-m=-a+$\frac{1}{2}$,解得:m=1,
∴f(x)=alnx-$\frac{x-1}{x+1}$,在区间(0,1)内是增函数,在f′(x)=$\frac{a}{x}$-$\frac{2}{(x+1)^{2}}$≥0,(0<x<1),…1分
即a(x+1)2-2x≥0,(0<x<1),
即a≥$\frac{2x}{(x+1)^{2}}$=$\frac{2}{x+\frac{1}{x}+2}$,(0<x<1),由x+$\frac{1}{x}$≥2$\sqrt{x×\frac{1}{x}}$=2,则$\frac{2}{x+\frac{1}{x}+2}$≤$\frac{1}{2}$,在x∈(0,1)内恒成立,
∴a≥$\frac{1}{2}$,
故实数a的取值范围为[$\frac{1}{2}$,+∞);
(2)证明:由函数g(x)=ex,则g′(x)=ex,过点P(b,eb),Q(-b,e-b),
作曲线C的切线方程为:l1:y=eb(x-b)+eb,l2:y=e-b(x-b)+e-b,
由l1与l2的交点为M(x0,y0),则$\left\{\begin{array}{l}{y={e}^{b}(x-b)+{e}^{b}}\\{y={e}^{-b}(x+b)+{e}^{-b}}\end{array}\right.$,…6分
消去y,解得:x0=$\frac{b({e}^{b}+{e}^{-b})-({e}^{b}-{e}^{-b})}{({e}^{b}-{e}^{-b})}$,…7分
∴x0=$\frac{b(1+{e}^{-2b})}{1-{e}^{-2b}}$-1,设e-2b=t,…8分
由b>0,则0<t<1,且lnt=-2b,于是-1=$\frac{2b}{lnt}$,…9分
∴x0=$\frac{2b}{lnt}$+$\frac{b(1+t)}{1-t}$=b($\frac{2}{lnt}$+$\frac{1+t}{1-t}$),…10分
由(1)知当a=$\frac{1}{2}$时,f(x)=$\frac{1}{2}$lnx-$\frac{x-1}{x+1}$在区间(0,1)上是增函数,…11分
∴f(t)=$\frac{lnt}{2}$-$\frac{t-1}{t+1}$<f(1)=0,即$\frac{lnt}{2}$<$\frac{t-1}{t+1}$,…12分
故$\frac{lnt}{2}$+$\frac{t-1}{t+1}$>0,…13分
已知b>0,则x0=b($\frac{2}{lnt}$+$\frac{1+t}{1-t}$)>0,
∴g(x0)>1.
点评 本题考查导数的综合应用,考查导数的几何意义,利用导数求函数的单调性及最值,考查换元法的应用,考查转化思想,属于中档题.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
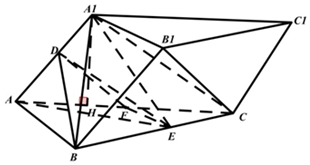 如图,在三棱锥ABC-A1B1C1中,侧面ACC1A1⊥底面ABC,∠A1AC=60°,AC=2AA1=4,点D,E分别是AA1,BC的中点.
如图,在三棱锥ABC-A1B1C1中,侧面ACC1A1⊥底面ABC,∠A1AC=60°,AC=2AA1=4,点D,E分别是AA1,BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既非充分又非必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com