练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    4．与向量$\overrightarrow a=（{4，3}）$方向相反的单位向量是$（{-\frac{4}{5}，-\frac{3}{5}}）$．

    分析 与向量$\overrightarrow a=（{4，3}）$方向相反的单位向量是-$\frac{\overrightarrow{a}}{|\overrightarrow{a}|}$．

    解答 解：与向量$\overrightarrow a=（{4，3}）$方向相反的单位向量是：
    -$\frac{\overrightarrow{a}}{|\overrightarrow{a}|}$=-$\frac{（4，3）}{\sqrt{16+9}}$=（-$\frac{4}{5}$，-$\frac{3}{5}$）．
    故答案为：（-$\frac{4}{5}$，-$\frac{3}{5}$）．

    点评 本题考查与已知向量方向相反的单位向量的求法，涉及到平面向量坐标运算法则等基础知识，考查运算求解能力，考查化归与转化思想，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

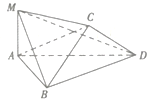    14．如图，将边长为2的正方形ABCD沿对角线BD折叠，使得平面ABD丄平面CBD，若AM丄平面ABD，且AM=$\sqrt{2}$
    （1）求证：DM⊥平面ABC；
    （2）求二面角C-BM-D的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．函数f（x）=（1-cos2x）cos2x，x∈R，设f（x）的最大值是A，最小正周期为T，则f（AT）的值等于（　　）
    A．$\frac{1}{4}$B．$\frac{1}{2}$C．1D．0

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．已知集合A={x|y=$\sqrt{x+1}$}，B={y=|y=1-ex}，则A∩B=（　　）
    A．[-1，1）B．[-1，1]C．（-1，1）D．（-∞，-1]∪[1，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．数列{an}中，a1=2，an+1=$\frac{n+1}{2n}{a}_{n}（n∈{N}^{*}）$．
    （Ⅰ）证明数列{$\frac{{a}_{n}}{n}$}是等比数列，并求数列{an}的通项公式；
    （Ⅱ）设bn=$\frac{{a}_{n}}{4n-{a}_{n}}$，若数列{bn}的前n项和是Tn，求证：Tn＜2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．若直线l经过点P（1，2），且垂直于直线2x+y-1=0，则直线l的方程是x-2y+3=0．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．在平面直角坐标平面内，已知A（0，5），B（-1，3），C（3，t）．
    （1）若t=1，求证：△ABC为直角三角形；
    （2）求实数t的值，使$|{\overrightarrow{AB}+\overrightarrow{AC}}|$最小；
    （3）若存在实数λ，使$\overrightarrow{AB}=λ•\overrightarrow{AC}$，求实数λ、t的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．已知双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的离心率为2，且右焦点到一条渐近线的距离为$\sqrt{3}$，双曲线的方程为（　　）
    A．$\frac{x^2}{4}-\frac{y^2}{3}=1$B．${x^2}-\frac{y^2}{3}=1$C．${y^2}-\frac{x^2}{3}=1$D．${x^2}-\frac{y^2}{4}=1$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．已知函数f（x）=alnx-m+$\frac{2}{x+1}$．g（x）=ex（其中e为自然对数的底数），函数f（x）在点（1，f（1））处的切线方程为y=（a-$\frac{1}{2}$）x-a+$\frac{1}{2}$．
    （1）若函数f（x）在（0，1）内是增函数，求实数a的取值范围．
    （2）当b＞0时，函数g（x）的图象C上有两点P（b，eb），Q（-b，e-b），过点P，Q作图象C的切线分别记为l1，l2，设l1与l2的交点为M（x0，y0），证明：g（x0）＞1．

    查看答案和解析>>

    同步练习册答案