
分析 (1)当t=1时,C(3,1),求出$\overrightarrow{AB},\overrightarrow{BC}$,由$\overrightarrow{AB}•\overrightarrow{BC}$=0,能证明△ABC为直角三角形.
(2)求出$\overrightarrow{AB}=(-1,-2),\overrightarrow{AC}=(3,t-5)$,从而$|{\overrightarrow{AB}+\overrightarrow{AC}}|=\sqrt{4+{{(t-7)}^2}}$,由此能求出结果.
(3)由$\overrightarrow{AB}=λ•\overrightarrow{AC}$,列出方程组,能求出实数λ、t的值.
解答 证明:(1)当t=1时,C(3,1),
则$\overrightarrow{AB}=(-1,-2),\overrightarrow{BC}=(4,-2)$…(2分)
∴$\overrightarrow{AB}•\overrightarrow{BC}=-1×4+(-2)×(-2)=0$,
∴$\overrightarrow{AB}⊥\overrightarrow{BC}$,
∴△ABC为直角三角形.…(4分)
解:(2)$\overrightarrow{AB}=(-1,-2),\overrightarrow{AC}=(3,t-5)$,
∴$\overrightarrow{AB}+\overrightarrow{AC}=(-1,-2)+(3,t-5)=(2,t-7)$…(6分)
∴$|{\overrightarrow{AB}+\overrightarrow{AC}}|=\sqrt{4+{{(t-7)}^2}}$
当t=7时,$|{\overrightarrow{AB}+\overrightarrow{AC}}|$的最小值为2.…(9分)
(3)由$\overrightarrow{AB}=λ•\overrightarrow{AC}$,得:
$(-1,-2)=λ•(3,t-5)⇒\left\{\begin{array}{l}-1=3λ\\-2=λ(t-5)\end{array}\right.$…(12分)
解是$\left\{\begin{array}{l}λ=-\frac{1}{3}\\ t=11\end{array}\right.$…(14分)
点评 本题考查三角形是直角三角形的证明,考查向量的模取最小值时对应的实数值的求法,涉及到平面向量坐标运算法则、向量垂直、向量的模等基础知识,考查运算求解能力,考查化归与转化思想,是基础题.


科目:高中数学 来源: 题型:选择题
| A. | (-∞,2) | B. | (0,1) | C. | (0,2) | D. | (1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 9 | C. | 10 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
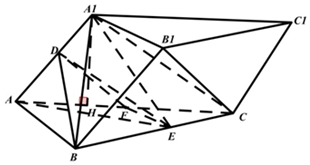 如图,在三棱锥ABC-A1B1C1中,侧面ACC1A1⊥底面ABC,∠A1AC=60°,AC=2AA1=4,点D,E分别是AA1,BC的中点.
如图,在三棱锥ABC-A1B1C1中,侧面ACC1A1⊥底面ABC,∠A1AC=60°,AC=2AA1=4,点D,E分别是AA1,BC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com