Question

2．桌面上放着3个半径为2014的球，两两相切，在它上方的空隙里放入一个球使其顶点（最高处）恰巧和 3个球的顶点在同一平面上，则该球的半径等于（　　）

• A． $\frac{2014}{3}$
• B． $\frac{2014}{9}$
• C． $\frac{4028}{3}$
• D． $\frac{4028}{9}$

Answer 1

分析 问题转化为摆放在桌面上的三个半径为1的球两两相切，在桌面与三球之间的空间中再摆入一个小球与三球和桌面都相切，我们可以分别设三个半径为1的球的球心分别为O₁，O₂，O₃，与桌面三个切点分别为A，B，C，构造一个正三棱柱，然后解三角形，即可得到答案．

解答 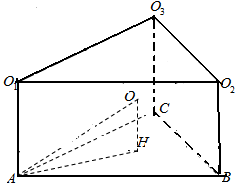解：问题转化为摆放在桌面上的三个半径为R的球两两相切，在桌面与三球之间的空间中再摆入一个小球与三球和桌面都相切，
设三个半径为R的球的球心分别为O₁，O₂，O₃，与桌面三个切点分别为A，B，C，如下图所示：
则三棱柱ABC-O₁O₂O₃，是一个底面边长为2R，高为R的正三棱柱，
则小球球心O在底面ABC上的投影必为△ABC的中心H，
设小球半径为r，
在△AOH中，AO=r+R，AH=2×$\frac{\sqrt{3}}{3}R$
则OH=$\sqrt{A{O}^{2}-A{H}^{2}}$，
又r+OH=R，解得r=$\frac{R}{3}$，
所以小球的半径等于$\frac{2014}{3}$；
故选A．

点评 本题考查的知识点是棱柱的结构特征，其中标出关键点，构造正三棱柱是解答本题的关键．