
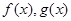 都在区间
都在区间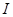 上有定义,对任意
上有定义,对任意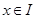 ,都有
,都有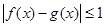 成立,则称函数
成立,则称函数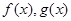 为区间
为区间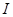 上的“伙伴函数”
上的“伙伴函数”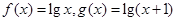 为区间
为区间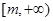 上的“伙伴函数”,求
上的“伙伴函数”,求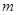 的范围。
的范围。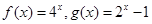 是否为区间
是否为区间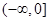 上的“伙伴函数”?
上的“伙伴函数”?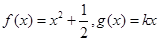 为区间
为区间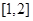 上的“伙伴函数”,求
上的“伙伴函数”,求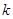 的取值范围
的取值范围 习题精选系列答案
习题精选系列答案科目:高中数学 来源:不详 题型:解答题
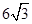 m2,为了使堤的上面与两侧面的水泥用料最省,要求断面的外周长(梯形的上底BC与两腰长的和)最小.如何设计防洪堤,才能使水泥用料最省.
m2,为了使堤的上面与两侧面的水泥用料最省,要求断面的外周长(梯形的上底BC与两腰长的和)最小.如何设计防洪堤,才能使水泥用料最省.
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
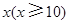 层,则每平方米的平均建筑费用为
层,则每平方米的平均建筑费用为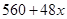 (单位:元).为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?
(单位:元).为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?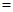 平均建筑费用
平均建筑费用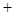 平均购地费用,平均购地费用
平均购地费用,平均购地费用 )
)查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
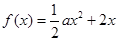 ,
,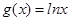 .
.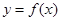 在
在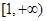 上是单调减函数,求
上是单调减函数,求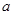 的取值范围;
的取值范围;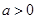 ,使得方程
,使得方程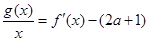 在区间
在区间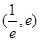 内有且只有两个不相等的实数根?若存在,请求出
内有且只有两个不相等的实数根?若存在,请求出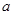 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com