
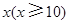 层,则每平方米的平均建筑费用为
层,则每平方米的平均建筑费用为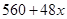 (单位:元).为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?
(单位:元).为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?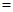 平均建筑费用
平均建筑费用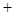 平均购地费用,平均购地费用
平均购地费用,平均购地费用 )
) 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源:不详 题型:解答题
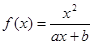 (a,b为常数)且方程f(x)-x+12=0有两个实根为x1="3," x2=4.
(a,b为常数)且方程f(x)-x+12=0有两个实根为x1="3," x2=4.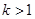 ,解关于x的不等式;
,解关于x的不等式;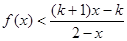 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
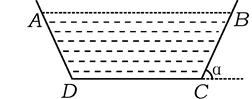
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
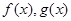 都在区间
都在区间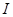 上有定义,对任意
上有定义,对任意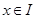 ,都有
,都有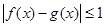 成立,则称函数
成立,则称函数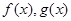 为区间
为区间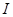 上的“伙伴函数”
上的“伙伴函数”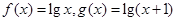 为区间
为区间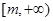 上的“伙伴函数”,求
上的“伙伴函数”,求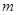 的范围。
的范围。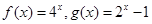 是否为区间
是否为区间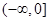 上的“伙伴函数”?
上的“伙伴函数”?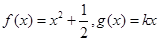 为区间
为区间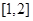 上的“伙伴函数”,求
上的“伙伴函数”,求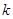 的取值范围
的取值范围查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
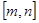 上有意义的两个函数
上有意义的两个函数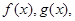 如果有任意
如果有任意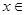
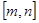 ,均有
,均有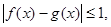 则称
则称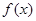 与
与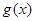 在
在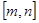 上是接近的,否则称
上是接近的,否则称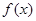 与
与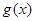 在
在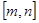 上是非接近的.现有两个函数
上是非接近的.现有两个函数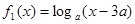 与
与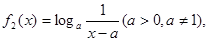 给定区间
给定区间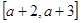 , 讨论
, 讨论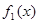 与
与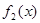 在给定区间
在给定区间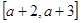 上是否是接近的.
上是否是接近的.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 在给定区间M上存在正数t,使得对于任意
在给定区间M上存在正数t,使得对于任意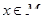 ,有
,有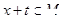 ,且
,且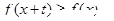 ,则称
,则称 为M上的t级类增函数。给出4个命题
为M上的t级类增函数。给出4个命题 上的3级类增函数
上的3级类增函数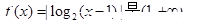 上的1级类增函数
上的1级类增函数 上的
上的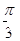 级类增函数,则实数a的最小值为2
级类增函数,则实数a的最小值为2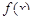 是定义
是定义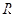 在上的函数,且满足:1.对任意
在上的函数,且满足:1.对任意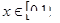 ,恒有
,恒有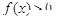 ;2.对任意
;2.对任意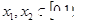 ,恒有
,恒有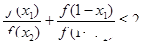 ;3. 对任意
;3. 对任意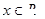 ,
,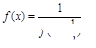 ,若函数
,若函数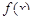 是
是 上的t级类增函数,则实数t的取值范围为
上的t级类增函数,则实数t的取值范围为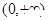 。
。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com