
分析 (1)当直线y=kx与圆相切时,k取得最值,利用切线的性质求出k;
(2)令z=y-x,则当直线y=x+z与圆相切时,截距取得最值,即z取得最值,利用切线的性质解出z的最值;
(3)x2+y2+2x+2y=6x+2y-1,令z=6x+2y-1,参考(2)的解法求出z的最值;
(4)m≥-x-2y,令z=-x-2y,参考(2)的解法求出z的最大值即可.
解答 解:设圆C:x2+y2-4x+1=0,即(x-2)2+y2=3.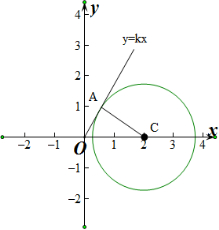
(1)设$\frac{y}{x}=k$,则当直线y=kx与圆C相切时,直线斜率最大或最小,即k最大或最小.
设直线y=kx与圆C切于第一象限内的点A,则AC=$\sqrt{3}$,OC=2,∴OA=1,
∴k=tan∠AOC=$\frac{AC}{OA}=\sqrt{3}$,
由图象的对称性可知当y=kx与圆C相切于第四象限内时,k=-$\sqrt{3}$.
∴$\frac{y}{x}$的最大值为$\sqrt{3}$,最小值为-$\sqrt{3}$.
(2)令z=y-x,则y=x+z,
∴当直线y=x+z与圆C相切时,z取得最大值或最小值.此时圆心到直线x-y+z=0的距离d=r=$\sqrt{3}$,
∴$\frac{|2+z|}{\sqrt{2}}=\sqrt{3}$,解得z=-2±$\sqrt{6}$.
∴y-x的最大值为-2+$\sqrt{6}$,最小值为-2-$\sqrt{6}$.
(3)∵x2+y2-4x+1=0,
∴x2+y2+2x+2y=4x-1+2x+2y=6x+2y-1,
令z=6x+2y-1,则y=-3x+$\frac{1+z}{2}$,
∴当直线y=-3x+$\frac{1+z}{2}$与圆C相切时,z取得最大值或最小值,此时圆心到直线6x+2y-1-z=0的距离d=r=$\sqrt{3}$,
∴$\frac{|11-z|}{2\sqrt{10}}=\sqrt{3}$,解得z=11±2$\sqrt{30}$,
∴x2+y2+2x+2y最大值是11+2$\sqrt{30}$,最小值是11-2$\sqrt{30}$.
(4)∵x+2y+m≥0,∴m≥-x-2y恒成立.
令z=-x-2y,则y=-$\frac{1}{2}x$-$\frac{z}{2}$.
∴当直线y=-$\frac{1}{2}x$-$\frac{z}{2}$与圆C相切时,z取得最大值或最小值,此时圆心到直线x+2y+z=0的距离d=r=$\sqrt{3}$,
.∴$\frac{|2+z|}{\sqrt{5}}=\sqrt{3}$,解得z=-2±$\sqrt{15}$,
∴-x-2y的最大值为-2+$\sqrt{15}$,
∴m≥-2+$\sqrt{15}$.
点评 本题考查了直线与圆的位置关系,简单的线性规划,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
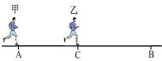 如图所示,甲从A地由静止匀加速跑向B地,当甲前进距离为x1时,乙从距A地x2处的C点由静止出发,加速度与甲相同,最后二人同时到达B地,则AB两地距离为( )
如图所示,甲从A地由静止匀加速跑向B地,当甲前进距离为x1时,乙从距A地x2处的C点由静止出发,加速度与甲相同,最后二人同时到达B地,则AB两地距离为( )| A. | x1+x2 | B. | $\frac{({x}_{1}+{x}_{2})^{2}}{4{x}_{1}}$ | ||
| C. | $\frac{{x}_{1}^{2}}{4({x}_{1}+{x}_{2})}$ | D. | $\frac{({x}_{1}+{x}_{2})^{2}}{({x}_{1}-{x}_{2}){x}_{1}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 26 | C. | 35 | D. | 36 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,1) | B. | [-1,1] | C. | [-1,1) | D. | (-∞,-1]∪[1,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com